■ 2009年09月14日 [OpenGL][GLSL][ゼミ] 第11回 拡散反射光による陰影
固定機能ハードウェアとプログラム可能ハードウェア
固定機能ハードウェアは処理内容をハードウェアで実装しているので, 同じ処理内容 (かつ, 同程度のハードウェア量・クロック) なら, 一般的にプログラム可能ハードウェアよりも高速です. しかし, ハードウェアで実装すると「できること」が決まってしまうので, 多様な処理に対応するために, ある程度汎用的に作っておかなければなりません. そのため, 処理内容によっては不要な手順が含まれてしまうことがあります. その点でプログラム可能ハードウェアは, 目的を達成するのに最適な手順が選択できるため, 同じ目的に対して固定機能ハードウェアより高速な処理が行える可能性があります.
陰影付けのおさらい
授業でやってる内容なので (まだの人もいるけど), どのあたりからおさらいを始めればいいのか悩ましいところですが, ざっと解説します. 適当に書いているので間違っているところがあるかもしれません. 教科書などで確認しておいてください.
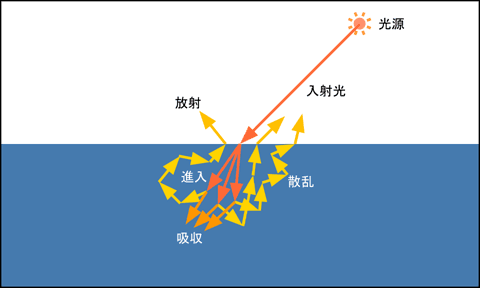
光源から物体表面 (屈折率の異なる媒質の境界面) に入射した光は, そこで正反射光と屈折光に分かれます. 屈折光は物体の内部に進入します. 一方, 正反射光は物体の表面で反射するので, 物体の内部には進入しません.
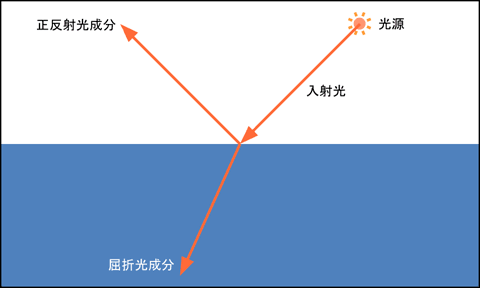
現実の物体表面には滑らかに見えても微小な凹凸があり, それによって反射方向や屈折方向が変化するので, 正反射光や屈折光の方向は多少なりとも分散します.
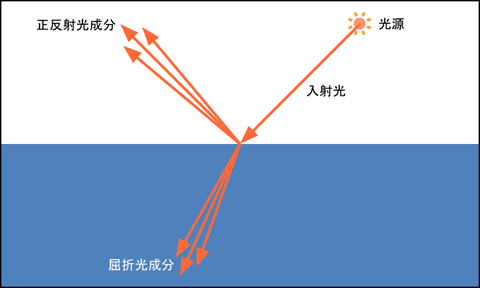
拡散反射光
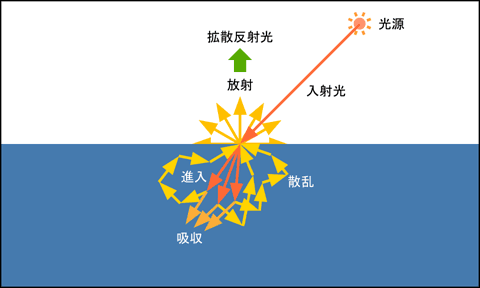
物体の内部に進入した光は, そこで散乱と吸収を繰り返し, 入射光の色成分のうち吸収されずに残ったものが, 再び光の入射位置から外部に放射され (ると考え) ます. この光を拡散反射光 (diffuse light) と呼びます. 吸収により拡散反射光には物体の色が付きます. この物体の色に相当する材質の特性 (material) を拡散反射係数と呼びます. また散乱により拡散反射光は指向性を失い, 全ての方向に均等に放射され (ると考え) ます (完全拡散反射面). なお, この考え方は金属には当てはまりません. 金属内に進入した光が, 散乱により外部に放出されることはありません (後述).
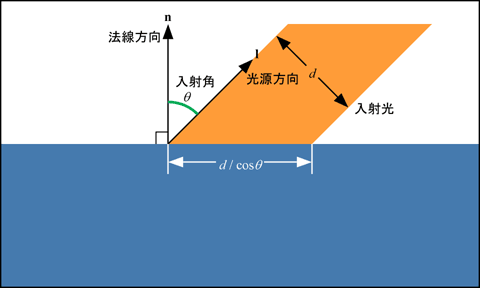
この拡散反射光の強度は, 入射光の強度に比例します. そして, 入射光の強度は, 入射の密度に比例します. いま, 幅 d の平行光線が入射角 θ で物体表面を照らしているとすれば, 入射光の照射面積は d /cosθ になります. 密度は面積に反比例しますから, 入射角 θ の入射光の密度は, 正面から入射した場合の cosθ 倍になります. これを Lambert の余弦法則と呼びます. ここで照射面の法線単位ベクトルを n, 照射点から光源方向を向いた光源方向単位ベクトルを l とすれば, cosθ = n⋅l となります. ただし, cosθ < 0 (θ < -π/2 または θ > π/2) の場合は, 光源が物体表面の「裏側」にあることになるので, 入射光の密度は 0 とします.
余談ですが, 現実の物体では, 拡散反射光が入射光の入射位置から放射されるという仮定は成り立ちません. 物体内に進入した光は物体内で散乱して, 入射位置からずれたところから放射されます (表面下散乱, subsurface scattering). これを正確に再現することは結構大変なので (計算時間がかかる), リアルタイムレンダリングでは入射位置から放射されるという仮定を用いるのが一般的です (局所表面下散乱, local subsurface scattering). 実際, このように仮定しても大抵うまくいくのですが, 光が透過する半透明の物体はうまく表現できません. 例えば, 牛乳が石膏のように見えたり, 人肌がコンシーラーを塗りたくったように見えたりしてしまいます.
鏡面反射光
入射光の正反射光のうち, 視点に届くものを鏡面反射光 (specular light) と呼びます. 正反射光は正反射方向を軸に分散しますので, 鏡面反射光の強度は視点方向 v がこの軸から離れるにしたがって小さくなります.
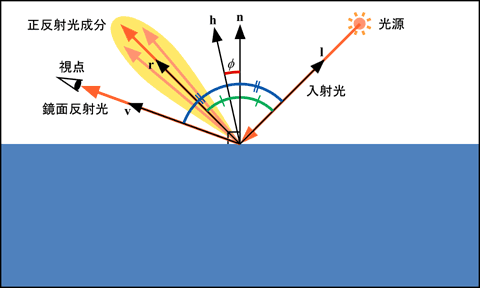
この割合を求めるには二通りの方法が用いられています. 一つは視点方向 v と正反射方向 r = 2(n⋅l)n - l のなす角にもとづく方法であり, もう一つは光源方向 l と視点方向 v の中間方向 h = (l + v) / |l + v| と照射面の法線 n のなす角 (φ) にもとづく方法です. 前者は光源の映り込みをモデル化したものと考えられ, 後者は物体表面の微小な凹凸によって入射光が視線方向に正反射される割合をモデル化したものだと考えられます.
同じことを表現するのに二通りの方法がある背景には, 光源を「点」でモデル化していることがあります. 実際の光源は「形」, すなわち光の放射面積を持っていますが, そのような光源を用いた陰影計算はやはり大変になるので (これも計算時間がかかる), リアルタイムレンダリングでは光源を点だと仮定するのが一般的です (平行光線も光源が無限遠にあると考えるので形は無限に小さくなって点になります). しかし, 光源が点だと光が出ているのに姿が見えないことになってしまいます. そこで正反射光に「広がり」を持たせる必要があるのですが, そのための方法が二通りあるということでしょう.
これにより, 前者の方法では球状の光源が映り込んだようなハイライトが得られるのに対して (下図左), 後者の方法では l と v が作る平面に沿った方向に伸びたハイライトが得られます (下図右). ハイライトを光源の映り込みだと捉えれば前者の方がそれらしい結果になりますが, 現実を観察してみると後者のような状況がよく見られます (濡れた路面のヘッドライトの映り込みが縦に伸びているとか). また, 物体表面の微小な凹凸をモデル化する微小面理論 (microfacet theory) は, 後者の考え方をベースにしています (というか, 微小面理論から後者の考え方が出てきた).


正反射光は物体の内部を通過していない (と考える) ので, 非金属の物質では物体の色の影響を受けることなく光源と同じ色になります. これに対して, 金属の正反射光には色が付く場合があります (金色とか銅赤色とか). 金属の反射光は, 金属表面のごく浅い部分にある自由電子が入射光のエネルギーによって共鳴振動を起こし, その振動エネルギーを放出することによって発生します (キリヤ: Q&A). このエネルギーの吸収と放出が入射光の波長に対して選択的に行われるために, 反射光に色が付く (分光分布が変化する) と考えられます. したがって, この場合は鏡面反射光に色をつけて表現します (下図左). この鏡面反射光に色を付ける材質の特性を鏡面反射係数と呼びます. 金属でなければ, 鏡面反射係数には通常グレー (入射光の分光分布を変化させない色) を用います (下図右).

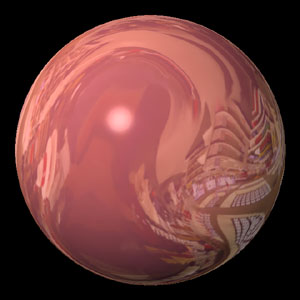
なお, 金属では拡散反射光が存在しませんが, 現実の金属には表面の汚れや腐食・酸化等による反射光や, 表面の微小な凹凸による正反射光の広がりなどによって拡散反射光 (のように見えるもの) が存在することがあります. また拡散反射光が全く無いと, (映り込みの処理をしない場合) 鏡面反射光が弱い部分が真っ黒になり, かえって不自然に見えてしまいます. そこで, 金属にも鏡面反射係数と似た色の拡散反射係数を設定する (ことによってごまかす) 場合があります.
鏡面反射係数と拡散反射係数の和が 1 を超えることは (通常) ありません (1 を超えたら入射光が増幅されることになります). この配分は Fresnel の式により入射光の入射角と波長に依存しますが, リアルタイムレンダリングでは一般的に定数が用いられます. ただし, 入射角が浅いときに鏡面反射光が強く出る現象 (Fresnel 反射) を再現する場合や, 微小面理論にもとづく陰影付けなどでは, Fresnel の式を取り入れます. また (陰影計算ではなく) 映り込みの処理により水面の表現を行う場合などでも, この配分を視線の入射角にしたがって変化させることがあります.
環境光
これまでは光源から照射点に直接届く直接光のみについて考えてきました. 照射点には直接光のほかに, 周囲の物体で1回以上反射した間接光も届きます. 間接光は直接光と異なり, 複数の複雑な経路を経ます.
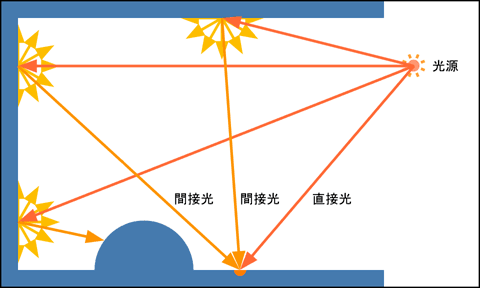
したがって照射点における陰影を正確に求めるには, 直接光・間接光の区別なく, その点に届く全ての光について視点方向に向かう反射光の強度を求め, それらの総和 (積分) を求める必要があります. また, この点から放射された光が他の点に届き, それがめぐりめぐって再びこの点に届くことも考慮しなければなりません.
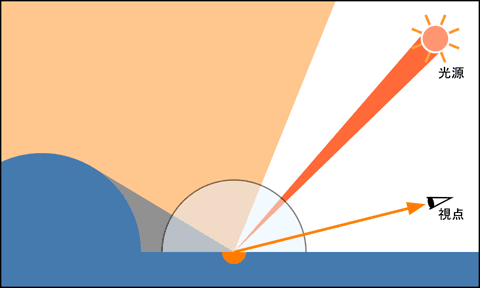
しかし, リアルタイムレンダリングではとてもそんなことしてられないので, 陰影を決める主要な要素である光源からの直接光のほかは, 環境光として定数にまとめてしまいます. ただし, これはかなりリアリティを損なう結果になります. 直接光が存在しなければ陰影は環境光によるものだけになりますが, これを定数にすると立体感が消えてしまいます.

照射点に到来する間接光の強さの方向分布は一様ではなく, また照射点の位置によっても変化するため, 間接光しか存在しない場合でも陰影は変化します. 例えば, 込み入ったところには光は届きにくいので, そのような領域は暗くなります.

このような陰影は大域照明 (global illumination) モデルを解くことによって得られます. しかしリアルタイムレンダリングでは, 複数の光源をシーン中の至る所に配置してそれらしく見せたりします.
リアリティの向上
リアルタイムレンダリングでは, これまで表面下散乱をはしょったり, 光源を点とみなしたり, 分光分布を赤・緑・青の三原色で表したり, 屈折率を定数にしたり, 環境光を定数にしたりして, 速度を稼いできました. しかし, このような「近似」を行った結果, 速度と引き換えにリアリティが犠牲になってしまいました. 速度とリアリティはトレードオフの関係にあります.
現在はグラフィックスハードウェアの性能や機能が大幅に向上したこともあって, リアリティを向上させる反面これまで時間がかかっていた処理をどうやってリアルタイムに実現するかというところが競われています. 前述の「近似」を行っていた対象に対しても, より精密な解をリアルタイムに求める手法が既にいくつも提案されています. 競争は激しいけど, やること (やれること) はまだいっぱいあります (と思いたい).
簡単な陰影付け
陰影計算には図形表面における法線ベクトルが必要になりますが, 今描いているのは半径 1 の単位球なので, 頂点の位置をそのままその点における法線ベクトルに使えます. また, 光源に向かうベクトル (光線ベクトル) が z 軸 (0, 0, 1) と一致していれば, 拡散反射光強度は光線単位ベクトルと法線単位ベクトルの内積に比例する (Lambert の余弦法則) ので, これは頂点の z 座標値になってしまいます. そこで, 試しにバーテックスシェーダで頂点の z 座標値を拡散反射色としてフラグメントシェーダに渡してみます.
バーテックスシェーダで vec3 型の varying 変数 diffuseColor を宣言し, これに頂点の座標値の z 成分 position.z を代入します. position.z は負の値になることがありますが, 今は気にしないことにします. vec3() によって diffuseColor の3つの要素の全てに同じ値が代入されます.
#version 120
//
// simple.vert
//
invariant gl_Position;
attribute vec3 position;
uniform mat4 projectionMatrix;
varying vec3 diffuseColor;
void main(void)
{
diffuseColor = vec3(position.z);
gl_Position = projectionMatrix * vec4(position, 1.0);
}
フラグメントシェーダでは, varying 変数 diffuseColor をそのまま gl_FragColor に出力します. gl_FragColor に代入された値は [0, 1] にクランプされるので, diffuseColor が負になっていても (多分) 問題ありません.
#version 120
//
// simple.frag
//
varying vec3 diffuseColor;
void main(void)
{
gl_FragColor = vec4(diffuseColor, 1.0);
}
これだけで, このような陰影を付けることができます.

光源方向の設定
それでは, 光源の方向 (光線ベクトル) を設定してみます. 光源の方向は, 例えば (10.0, 6.0, 3.0) とします. このベクトルを GLSL の組み込み関数 normalize() を使って正規化し, vec3 型の const 変数 (というか定数) lightDirection に格納しておきます. これと面の法線ベクトル position との内積を求めます. ベクトルの内積には GLSL の組み込み関数 dot() を用います.
#version 120
//
// simple.vert
//
invariant gl_Position;
attribute vec3 position;
uniform mat4 projectionMatrix;
varying vec3 diffuseColor;
const vec3 lightDirection = normalize(vec3(10.0, 6.0, 3.0));
void main(void)
{
diffuseColor = vec3(dot(position, lightDirection));
gl_Position = projectionMatrix * vec4(position, 1.0);
}
この正規化は main() の外で宣言している const 変数の初期化の際に行っているので, シェーダプログラムの呼び出しのたびに行われることは多分ない (ので, シェーダの負荷にはならない) と思うのですが, GLSL のコンパイラがどんなコードを吐いているのかは知りません.

色の設定
次に, 光源の色と物体表面の色 (拡散反射係数) を設定してみます. 拡散反射光の放射輝度 (radiance) Ld は光源の放射照度 (irradiance) を EL, 光線の入射角を θi, 物体表面の拡散反射色を cd とするとき, Ld = (cd /π) EL cosθi で求められます. ここで cosθi = n⋅l です. また, 面倒なので kd = cd /π とし, これを拡散反射係数とします.
kd や EL は光の三原色 RGB ごとに指定します. で, これらに設定する値なんですが, ちょっと気をつけなければいけないことがあります. 前に gl_FragColor に代入された値は [0, 1] にクランプされると説明しましたが, このために, ここで計算する放射輝度 Ld がこの範囲に収まるようにしなければなりません. gl_FragColor に 0 を設定すると, 表示装置 (ディスプレイ) には最も暗い色が表示され, 1 を設定すれば最も明るい色が設定されます. しかし, 現実の世界にある「明るさ」を, 表示装置が全て表示可能なわけではありません. したがって, 現実の世界での「値」を直接 kd や EL に設定すると, 表示装置上で明るさが飽和してしまったり, 逆に暗くなりすぎたりしてしまいます. もちろん, これを回避する手法 (HDR レンダリング) も提案されていますが, OpenGL の固定機能ハードウェアでは, これらの値の範囲を [-1, 1] の範囲にクランプするという手段を採用していました.
じゃあ, ここではどうするかなんですけど, とりあえず kd は [0, 1] の間で設定すべきでしょう. 一方 EL は, おそらくとても大きな値を設定すべきだと思いますが, そうすると計算結果を gl_FragColor が許容できる範囲に収めるために, kd を十分小さくする必要があります. これは, 直接光の放射照度が間接光の放射照度に比べてずっと小さい (ことが多い) と考えれば合理的ですが, これらの値は計算結果が飽和しないように慎重に決めなければなりません.
そこで, やっぱりめんどくさいので, ここでも光源の (放射照度ではなく) 「明るさ」を [0, 1] の範囲で設定することにしたいと思います. ああ, 気弱だ.光源の明るさを黄色 (1.0, 1.0, 0.0) として const 変数 lightColor に設定し, 拡散反射係数 kd をシアン (0.0, 1.0, 1.0) として const 変数 diffuseMaterial に設定します. そして, 陰影を計算する際に, これらを掛け合わせます.
#version 120
//
// simple.vert
//
invariant gl_Position;
attribute vec3 position;
uniform mat4 projectionMatrix;
varying vec3 diffuseColor;
const vec3 lightDirection = normalize(vec3(10.0, 6.0, 3.0));
const vec3 lightColor = vec3(1.0, 1.0, 0.0);
const vec3 diffuseMaterial = vec3(0.0, 1.0, 1.0);
void main(void)
{
diffuseColor = vec3(dot(lightDirection, position)) * lightColor * diffuseMaterial;
gl_Position = projectionMatrix * vec4(position, 1.0);
}
すると, こういう色になります.

光源の情報
材質の情報 (拡散反射係数しかないけど) や光源の情報は, 今のところシェーダプログラムに埋め込んでいます. 材質の情報はシェーダプログラムに埋め込んでしまっても構わないと思いますけど, 光源の情報は複数のシェーダプログラムの間で共有することが多いでしょうから, これは少し都合が悪いかも知れません. そこで, 光源の情報はアプリケーションプログラムから設定するようにします.
まず, バーテックスシェーダで光源の方向と位置を設定している const 変数 lightDirection と lightColor を uniform 変数に変更します. もちろん, これらを初期化している値は削除します.
#version 120
//
// simple.vert
//
invariant gl_Position;
attribute vec3 position;
uniform mat4 projectionMatrix;
varying vec3 diffuseColor;
uniform vec3 lightDirection;
uniform vec3 lightColor;
const vec3 diffuseMaterial = vec3(0.0, 1.0, 1.0);
void main(void)
{
diffuseColor = vec3(dot(lightDirection, position)) * lightColor * diffuseMaterial;
gl_Position = projectionMatrix * vec4(position, 1.0);
}
次に, メインプログラムで, 光源の方向と色を保持する配列変数 lightDirection と lightColor を宣言します. 光源の方向は正規化しておきます. 光源の色は, 今度は白にします. また, uniform 変数の場所を保持する変数 lightDirectionLocation と lightColorLocation も宣言しておきます.
...
/*
** 図形
*/
static GLuint points;
extern GLuint wireCube(const GLuint *buffer);
extern GLuint wireSphere(int slices, int stacks, const GLuint *buffer);
extern GLuint solidSphere(int slices, int stacks, const GLuint *buffer);
/*
** 光源
*/
static GLfloat lightDirection[] = { 0.83f, 0.50f, 0.25f };
static GLfloat lightColor[] = { 1.0f, 1.0f, 1.0f };
static GLint lightDirectionLocation, lightColorLocation;
/*
** 画面表示
*/
...
そして, シェーダプログラムをリンクした後に lightDirectionLocation と lightColorLocation に uniform 変数の場所を保存しておきます.
...
/*
** 初期化
*/
static void init(void)
{
...
/* uniform 変数 projectionMatrix の場所を得る */
projectionMatrixLocation = glGetUniformLocation(gl2Program, "projectionMatrix");
/* uniform 変数 lightDirection の場所を得る */
lightDirectionLocation = glGetUniformLocation(gl2Program, "lightDirection");
/* uniform 変数 lightDirection の場所を得る */
lightColorLocation = glGetUniformLocation(gl2Program, "lightColor");
/* 頂点バッファオブジェクトを2つ作る */
glGenBuffers(2, buffer);
...
最後に, 描画の際, シェーダプログラムを適用した後に, unform 変数 (の場所) に対して値を設定します.
...
/*
** 画面表示
*/
static void display(void)
{
...
/* シェーダプログラムを適用する */
glUseProgram(gl2Program);
/* uniform 変数 projectionMatrix に行列を設定する */
glUniformMatrix4fv(projectionMatrixLocation, 1, GL_FALSE, projectionMatrix);
/* uniform 変数 lightDirection に光源の方向を設定する */
glUniform3fv(lightDirectionLocation, 1, lightDirection);
/* uniform 変数 lightColor に光源の色を設定する */
glUniform3fv(lightColorLocation, 1, lightColor);
/* index が 0 の attribute 変数に頂点情報を対応付ける */
glEnableVertexAttribArray(0);
...
- void glUniform3fv(GLint location, GLsizei count, const GLfloat *value);
- vec3 型の uniform 変数に値を格納します. location は glGetUniformLocation() で得られた uniform 変数の場所を指定します. count はデータの個数です. 格納する uniform 変数が配列なら, その要素数までの数が指定できます. 普通の変数なら 1 です. value は uniform 変数に格納するデータの配列です. vec3 型の uniform 変数の要素数は 3 ですから, この配列の要素数は count * 3 個になります.
ここらでとりあえずひと区切り付けます.
いつもサイトのほう参考にさせていただいております。<br>Windows版ですが、ファイル名の関係で直リンクが切れておりましたので、ご報告させていただきます。
ryo さま、ご連絡ありがとうございます。どうもファイルそのものを失っているようなのですが、今更 LZH でアーカイブ作るのも微妙な気がしますので、ちょっと考えさせてください。できるだけ早く対応させていただきます。よろしくお願いいたします。
かってに参考にさせていただいております。 <br>windows版のファイルのリンク切れですが、リンク先は以下ではないでしょうか。lzhとzip 拡張子が違っていませんか。 <br>https://marina.sys.wakayama-u.ac.jp/~tokoi/summer/summer08.zip <br>