床井研究室

球面線形補間

４月に入ってなんだか妙に忙しいと思っているうちに，今日はもう３０日！なのに，今月は全然ブログ書いとらん…いかん，何か書かねばと思ってもネタがない．仕方がないからゲームグラフィックス特論（なんちゅう講義名だ）の宿題のヒントを．

まず，２つのクォータニオンの補間の実装は，例えばこんな具合になります．

#include <math.h>
#include <float.h>
 
/*
** 球面線形補間 p ← q と r を t で補間したクォータニオン
*/
void slerp(double p[], const double q[], const double r[],
           const double t)
{
  double qr = q[0] * r[0] + q[1] * r[1] + q[2] * r[2] + q[3] * r[3];
  double ss = 1.0 - qr * qr, sp;
  
  if (ss <= 0.0 || (sp = sqrt(ss)) == 0.0) {
    p[0] = q[0];
    p[1] = q[1];
    p[2] = q[2];
    p[3] = q[3];
  }
  else {
    double ph = acos(qr);
    double pt = ph * t;
    double t1 = sin(pt) / sp;
    double t0 = sin(ph - pt) / sp;
    
    p[0] = q[0] * t0 + r[0] * t1;
    p[1] = q[1] * t0 + r[1] * t1;
    p[2] = q[2] * t0 + r[2] * t1;
    p[3] = q[3] * t0 + r[3] * t1;
  }
}

宿題のプログラムを完成させるのに必要なのは，時間軸上に配置された複数のクォータニオンを補間して，ある時刻における姿勢を求める手続きです．すなわち，時刻 t_i における姿勢 q_i が与えられているとき，それらから時刻 t における姿勢 q(t) を求める関数を作ります．

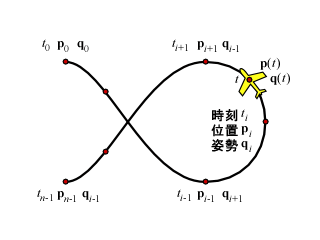
このために，まず t を含む区間 [t_i,t_i+i) を探します．これには飛行経路を求めるのに使っているスプライン補間同様，二分探索を用いることができます．そして，その区間 i の両端のクォータニオン q_i と q_i+1 を線形補間して，q(t) を求めます．書いてみると簡単でしょ＞某氏．

/*
** 複数のクォータニオン間の球面線形補間（折れ線）
**   p ← t[i] におけるクォータニオン q[i], 0 <= i < n に対する
**        u における補間値
**        
*/
void mslerp(double p[],
            const double t[], const double q[][4], const int n,
	    const double u)
{
  int i = 0, j = n - 1;
  
  /* u を含む t の区間 [t[i], t[i+1]) を二分法で求める */
  while (i < j) {
    int k = (i + j) / 2;
    if (t[k] < u)
      i = k + 1;
    else
      j = k;
  }
  if (i > 0) --i;
  
  slerp(p, q[i], q[i + 1], (u - t[i]) / (t[i + 1] - t[i]));
}

それで，たとえばこういう絵を作ってみてください．

（しかし線形補間だとやっぱりぎこちない）