■ 2004年08月30日 [OpenGL] 押し出し
夏休みはどこだ
7月から8月にかけて例年に無く忙しくて(独立法人化の影響?),ついに7月はブログに何も書けませんでした.そればかりか,このままでは8月も何も書けずに終わってしまいそうです.ということで,以前,学生さんにサンプルプログラムを書いてやると約束したまま放置していた「押し出し」について,ちょいと書いてみます.
卒業研究の指導なんかをしていると,毎年,同じようなところで学生さんが引っかかっているのを目にします.でも,たいていはテクスチャマッピングに使う画像ファイルの読み出し方のような,研究の本筋とはあんまり関係なさそうなところなんで,自分で解決してくれることを期待してほったらかしにしておきます(本当は面倒だからという可能性大).とは言っても,毎年同じところで時間を食ってしまっているのも効率が悪い気がします.ましてや,このブログはそういう小ネタをストックしていこうと思って作ったんだし…
押し出し
押し出し (extrusion) は平面図形を移動したときの軌跡によって立体形状を表現するものです.掃引 (sweep) ともいい,たいていの CG ソフトに用意されている基本的な形状定義手法です.OpenGL では,GLE Tubing and Extrusion Library を使えばこのような形状を描くことができます.また VRML にもExtrusion というノードが用意されています.3次元の曲線や折れ線に対して太さをもたせたパイプのようなものも,この押し出しによって作成することができます.
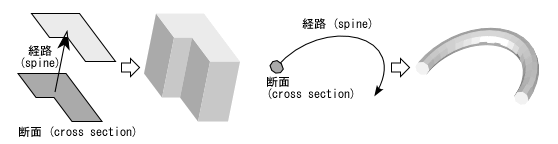
ここでは,VRML の Extrusion ノードのサブセットを実現する,押し出しの実装を考えてみます.GLE があるので自分で作る意味はないのですが,この実装の中に学生さんに押さえておいてほしいなぁと思うポイントがいくつかあったので,恥を忍んで?書いてみます.
関数 extrusion() は,押し出す平面図形,すなわちこの立体形状の断面形状 (cross section) と,この図形を押し出す経路 (spine,背骨) をもとに,押し出し形状を作成して描画するものとします.この断面と経路は,いずれも折れ線の節点の座標値の配列で表します.
/* ** 押し出し ** cs: 断面形状 (cross section) ** nc: 断面の頂点数 ** sp: 押し出す経路 (spine) ** ns: 経路の節点の数(起点と終点を含む) */ void extrusion(const double cs[][2], int nc, const double sp[][3], int ns)
ここで断面形状は xy 平面上に置くものとします.したがって断面の頂点座標値は,Z 値を省略して (z = 0) 2次元座標で表すことにします.
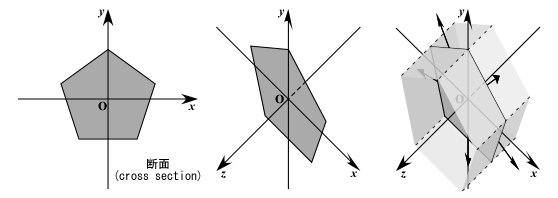
また,断面の各辺の法線単位ベクトルを求めておきます.これはこの断面を Z 軸方向に押し出したときの,側面の法線ベクトルになります.
double n[MAXCS][2]; /* 断面の法線ベクトル */
...
/* 断面の法線ベクトルを求める (z = 0) */
for (i = 1; i < nc; ++i) {
double x = cs[i][0] - cs[i - 1][0];
double y = cs[i][1] - cs[i - 1][1];
double d = x * x + y * y;
if (d != 0.0) {
double a = sqrt(d);
n[i][0] = y / a;
n[i][1] = -x / a;
}
}
ベクトルの方向転換
次に,この断面を経路の方向に回転する方法について考えます.ある単位ベクトル u の方向を,別の単位ベクトル v の方向に回転する場合,この回転の軸の方向単位ベクトルは n = u×v/|u×v| になります.
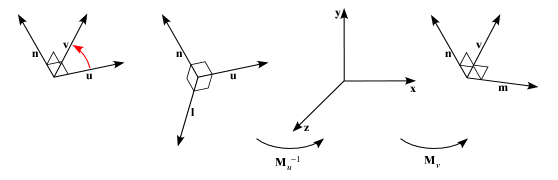
そこで,まず u と n に直交するベクトル l = u×n/|u×n| を求めます.このとき x = (1, 0, 0), y = (0, 1, 0), z = (0, 0, 1) をそれぞれ u, n, l に移す変換は,Mu = (u n l)T となります.同様に, v と n に直交するベクトル m = v×n/|v×n| を求めます.このとき x, y, z をそれぞれ v, n, m に移す変換は,Mv = (v n m)T となります.
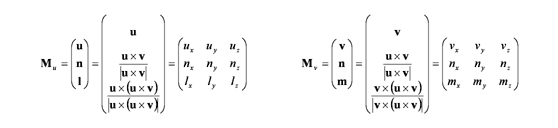
これより,ある単位ベクトル u の方向を,別の単位ベクトル v の方向に回転する変換は,Mr = Mu-1Mv = MuTMv となります.
/*
** ベクトルの方向転換
** ベクトル u をベクトル v 方向に向ける変換行列を r に格納する
*/
static void turn(const double u[], const double v[], double r[])
{
double d, n[3];
/* 共通の軸(回転軸)n = u×v */
n[0] = u[1] * v[2] - u[2] * v[1];
n[1] = u[2] * v[0] - u[0] * v[2];
n[2] = u[0] * v[1] - u[1] * v[0];
/* n の長さ */
d = n[0] * n[0] + n[1] * n[1] + n[2] * n[2];
if (d == 0.0) {
/* 回転しない */
r[1] = r[2] = r[3] = r[5] = r[6] = r[7] = 0.0;
r[0] = r[4] = r[8] = 1.0;
}
else {
/*
** r : (u, n, u×n) → (x, y, z) の変換行列
** s : (x, y, z) → (v, n, v×n) の変換行列
*/
double s[9];
double a = sqrt(d);
/* t を y軸の成分とする */
r[1] = s[3] = n[0] / a;
r[4] = s[4] = n[1] / a;
r[7] = s[5] = n[2] / a;
/* u側のx軸 u */
a = sqrt(u[0] * u[0] + u[1] * u[1] + u[2] * u[2]);
r[0] = u[0] / a;
r[3] = u[1] / a;
r[6] = u[2] / a;
/* v側のx軸 v */
a = sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
s[0] = v[0] / a;
s[1] = v[1] / a;
s[2] = v[2] / a;
/* u側のz軸 l = u×n */
r[2] = u[1] * n[2] - u[2] * n[1];
r[5] = u[2] * n[0] - u[0] * n[2];
r[8] = u[0] * n[1] - u[1] * n[0];
a = sqrt(r[2] * r[2] + r[5] * r[5] + r[8] * r[8]);
r[2] /= a;
r[5] /= a;
r[8] /= a;
/* v側のz軸 m = v×n */
s[6] = v[1] * n[2] - v[2] * n[1];
s[7] = v[2] * n[0] - v[0] * n[2];
s[8] = v[0] * n[1] - v[1] * n[0];
a = sqrt(s[6] * s[6] + s[7] * s[7] + s[8] * s[8]);
s[6] /= a;
s[7] /= a;
s[8] /= a;
/* r ← r s */
multiply(r, s, r);
}
なお,この変換は押し出しに限らず,視点の移動や,ある軌跡に沿って向きを変えながら物体を移動させる場合など,様々なところで利用できます.
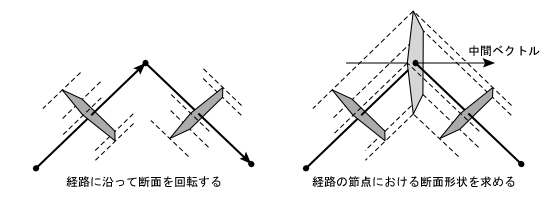
断面のせん断変形
断面を経路の方向に回転する変換を求めたら,これを用いて経路の節点における断面形状を求めます.節点の断面は,節点の進入側の経路と退出側の経路の中間ベクトルを法線ベクトルにもつ平面上にあり,その形状はもとの断面形状をせん断変形したものになります.
まず,この中間ベクトル h を最初の断面の空間に移します.このベクトル h' は,断面を進入側の経路の向きに回転する変換を Mr とすれば,h' = h MrT で求めることができます.ここで h' = (a, b, c) とおけば,原点を通り h' を法線ベクトルとする平面の方程式は ax + by + cz = 0 になります.この平面に xy 平面上の図形を投影する変換は (x, y, z - (ax + by) / c) になります.この変換は,次のような行列で表すことができます.
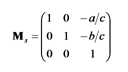
したがって,xy 平面上の断面形状を Ms で変形し,それを Mr で経路の向きに向けた後,節点の位置に平行移動すれば,節点における断面形状を得ることができます.
/*
** 押し出し
** cs: 断面形状 (cross section)
** nc: 断面の頂点数
** sp: 押し出す経路 (spine)
** ns: 経路の節点の数(起点と終点を含む)
*/
void extrusion(const double cs[][2], int nc, const double sp[][3], int ns)
{
if (--ns > 0) {
double v[2][3], a; /* 接点に進入・退出する線分の方向ベクトルと長さ */
double p[2][MAXCS][3]; /* 接点における断面の頂点位置 */
double n[MAXCS][2]; /* 断面の法線ベクトル */
double m[9], r[9]; /* 変換行列 */
int i, k = 0;
/* あんまり頂点数の多い断面は切り詰める */
if (nc > MAXCS) nc = MAXCS;
/* 断面の法線ベクトルを求める (z = 0) */
for (i = 1; i < nc; ++i) {
double x = cs[i][0] - cs[i - 1][0];
double y = cs[i][1] - cs[i - 1][1];
double d = x * x + y * y;
if (d != 0.0) {
double a = sqrt(d);
n[i][0] = y / a;
n[i][1] = -x / a;
}
}
/* 断面の軸ベクトル */
v[0][0] = 0.0;
v[0][1] = 0.0;
v[0][2] = 1.0;
/* 起点の進入側の方向ベクトルは退出側の方向ベクトルと一致させる */
v[1][0] = sp[1][0] - sp[0][0];
v[1][1] = sp[1][1] - sp[0][1];
v[1][2] = sp[1][2] - sp[0][2];
a = sqrt(v[1][0] * v[1][0] + v[1][1] * v[1][1] + v[1][2] * v[1][2]);
v[1][0] /= a;
v[1][1] /= a;
v[1][2] /= a;
/* 断面を起点における進入側の方向ベクトルの向きに回転する行列 m */
turn(v[0], v[1], m);
transform(cs, nc, m, sp[0], p[1]);
/* 起点の断面を描く */
cap(p[1], nc - 1, 0, v[1]);
for (i = 1; i < ns; ++i) {
double h[3]; /* 中間ベクトル */
/* 退出側の方向ベクトル */
v[k][0] = sp[i + 1][0] - sp[i][0];
v[k][1] = sp[i + 1][1] - sp[i][1];
v[k][2] = sp[i + 1][2] - sp[i][2];
a = sqrt(v[k][0] * v[k][0] + v[k][1] * v[k][1] + v[k][2] * v[k][2]);
v[k][0] /= a;
v[k][1] /= a;
v[k][2] /= a;
/* 中間ベクトル=断面の法線ベクトル */
h[0] = v[k][0] + v[1 - k][0];
h[1] = v[k][1] + v[1 - k][1];
h[2] = v[k][2] + v[1 - k][2];
/* 中間ベクトル h に直交する断面を求める変換 r */
shear(h, m, r);
/* 中間ベクトル h における断面形状を求める */
transform(cs, nc, r, sp[i], p[k]);
/* 側面を描く */
side(p[1 - k], p[k], n, nc, m);
/* 進入側の方向ベクトルを退出側の方向ベクトルに回転する行列 r */
turn(v[1 - k], v[k], r);
/* 断面を退出側の方向ベクトルの向きに回転する行列 m */
multiply(m, r, m);
/* 進入側と退出側を入れ替える */
k = 1 - k;
}
/* 終点の断面はひとつ前の断面と同じ向きで位置のみが異なる */
transform(cs, nc, m, sp[ns], p[k]);
/* 側面を描く */
side(p[1 - k], p[k], n, nc, m);
/* 終点の断面を描く */
cap(p[k], 0, nc - 1, v[1 - k]);
}
}
うーん,なんだか完備した説明にならないなぁ.これではわかりにくいだろうなぁ.多分,後で自分で読んでもわからん気がする.やっぱりソースを読んでください.
>ある単位ベクトル u の方向を,別の単位ベクトル v の方向に回転する変換は,Mr = Mu-1Mv = MuTMv <br><br>この変換についてご教示ください。<br>このMuの逆行列Mu-1はいったい何を意味しているのですか?<br>変換Mは、Mvを行った後、Mv-1を行うという理解でよろしいでしょうか?<br>なぜこの操作手順で変換を行うことになるのかが理解できません。<br>ご教示のほどよろしくお願いします。