床井研究室

今までにあった質問

かなり以前，「『視点を移動するのではなく，物体をぐるぐる回す方法は？』に書いてある方法では思ったとおり回転できない」という指摘を受けました．

確かにそのとおりなんですが，もとより「手抜き」の方法ですし（言い訳），まともな方法が GLUT のサンプルなどに含まれている trackball.c や「宇治社中」さんあたりにあると思ってたんで，そのままにしてました．でも，自分が作っているもので使ってみて思ったとおり回転できないことがあるのはやっぱり面白くなかったので，ひとつまじめに考えてみました．

クォータニオンを使ってみる

変換（行列）を累積的に合成するなんてことをするとロクな目にあわない気がしたので，ああいう手を抜いた実装になってたんですが，オブジェクトの「今見えている状態」に対してさらに回転を加えようと思えば，やはり避けて通ることはできません．そこで，回転をクォータニオンを使って表すことにします．そのために，まずクォータニオンの積と，クォータニオンから回転の変換行列を求める関数を用意しておきます．クォータニオンについて勉強したければ，金谷先生の本をどうぞ．

/*
** クォータニオンの積 r <- p x q
*/
void qmul(double r[], const double p[], const double q[])
{
  r[0] = p[0] * q[0] - p[1] * q[1] - p[2] * q[2] - p[3] * q[3];
  r[1] = p[0] * q[1] + p[1] * q[0] + p[2] * q[3] - p[3] * q[2];
  r[2] = p[0] * q[2] - p[1] * q[3] + p[2] * q[0] + p[3] * q[1];
  r[3] = p[0] * q[3] + p[1] * q[2] - p[2] * q[1] + p[3] * q[0];
}
  
/*
** 回転の変換行列 r <- クォータニオン q
*/
void qrot(double r[], double q[])
{
  double x2 = q[1] * q[1] * 2.0;
  double y2 = q[2] * q[2] * 2.0;
  double z2 = q[3] * q[3] * 2.0;
  double xy = q[1] * q[2] * 2.0;
  double yz = q[2] * q[3] * 2.0;
  double zx = q[3] * q[1] * 2.0;
  double xw = q[1] * q[0] * 2.0;
  double yw = q[2] * q[0] * 2.0;
  double zw = q[3] * q[0] * 2.0;
  
  r[ 0] = 1.0 - y2 - z2;
  r[ 1] = xy + zw;
  r[ 2] = zx - yw;
  r[ 4] = xy - zw;
  r[ 5] = 1.0 - z2 - x2;
  r[ 6] = yz + xw;
  r[ 8] = zx + yw;
  r[ 9] = yz - xw;
  r[10] = 1.0 - x2 - y2;
  r[ 3] = r[ 7] = r[11] = r[12] = r[13] = r[14] = 0.0;
  r[15] = 1.0;
}

また，現在の回転を表すクォータニオン cq と，マウスのドラッグ中の回転を表すクォータニオン tq を用意します．cq の初期値は単位クォータニオンにしておきます．

/* 回転の初期値とドラッグ中の回転 (クォータニオン) */
static double cq[4] = { 1.0, 0.0, 0.0, 0.0 };
static double tq[4];

このほか，オブジェクトの回転に使う変換行列 rt を用意しておきます．

/* 回転の変換行列 */
static double rt[16];

この行列の初期値は単位行列にしておきます．cq は最初単位クォータニオンなので，これを使うこともできます．

void init (void)
{
  ...
  
  /* 回転行列の初期化 */
  qrot(rt, cq);
}

マウスのドラッグにしたがって物体を回転させるためには，ドラッグ中のマウスの移動方向と移動量を検出する必要があります．そこで，マウスボタンを押したときにマウスの位置（ドラッグ開始点）を記録します．また，マウスボタンを離したときにはドラッグ中の回転のクォータニオンの内容を回転の初期値のクォータニオンに保存して，現在のオブジェクトの回転を「固定」します．

/* ドラッグ開始位置 */
static int cx, cy;
  
...
  
void idle(void)
{
  glutPostRedisplay();
}
  
void mouse(int button, int state, int x, int y)
{
  switch (button) {
  case GLUT_LEFT_BUTTON:
    switch (state) {
    case GLUT_DOWN:
      /* ドラッグ開始点位置を記録する */
      cx = x;
      cy = y;
      /* アニメーション開始 */
      glutIdleFunc(idle);
      break;
    case GLUT_UP:
      /* アニメーション終了 */
      glutIdleFunc(0);
      /* ドラッグ終了時の回転を保存する */
      cq[0] = tq[0];
      cq[1] = tq[1];
      cq[2] = tq[2];
      cq[3] = tq[3];
      break;
    default:
      break;
    }
    break;
  default:
    break;
  }
}

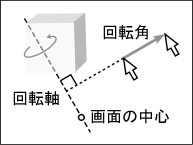
マウスのドラッグ中には，現在のマウスポインタの位置のドラッグ開始点からの変位から回転軸ベクトルと回転角を求め，回転のクォータニオンを求めます．これにオブジェクトの現在の回転のクォータニオンを掛け，ドラッグ中の回転を表すクォータニオンを求めます．これを回転の変換行列に直します．

このとき回転量がウィンドウのサイズに依存しないように，マウスポインタの変位をウィンドウ内の相対的な位置に変換しておいたほうがいいでしょう．このためにウィンドウのサイズからスケールファクタ sx, sy を求めておきます．定数 SCALE はマウスポインタの位置から回転角への換算に用います．これを 2π にしておけば，マウスポインタをウィンドウの幅（あるいは高さ）分移動したときに，物体をちょうど一回転させることができます．

/* マウスの絶対位置→ウィンドウ内での相対位置の換算係数 */
static double sx, sy;
  
/* マウスの相対位置→回転角の換算係数 */
#define SCALE (2.0 * 3.14159265358979323846)
  
...
  
void resize(int w, int h)
{
  /* マウスポインタ位置のウィンドウ内の相対的位置への換算用 */
  sx = 1.0 / (double)w;
  sy = 1.0 / (double)h;
  
  ...
}
  
...
  
void motion(int x, int y)
{
  /* マウスポインタの位置のドラッグ開始位置からの変位 (相対値) */
  double dx = (x - cx) * sx;
  double dy = (y - cy) * sy;
  
  /* マウスポインタの位置のドラッグ開始位置からの距離 (相対値) */
  double a = sqrt(dx * dx + dy * dy);
  
  if (a != 0.0) {
    /* マウスのドラッグに伴う回転のクォータニオン dq を求める */
    double ar = a * SCALE * 0.5;
    double as = sin(ar) / a;
    double dq[4] = { cos(ar), dy * as, dx * as, 0.0 };
    
    /* 回転の初期値 cq に dq を掛けて回転を合成する */
    qmul(tq, dq, cq);
    
    /* クォータニオンから回転の変換行列を求める */
    qrot(rt, tq);
  }
}

あとは，求めた回転の変換行列を用いて，図形を描画します．

void display(void)
{
  ...
  
  glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
  
  /* モデルビュー変換行列の初期化 */
  glLoadIdentity();
  
  /* 視点の移動 */
  gluLookAt(ex, ey, ez, tx, ty, tz, 0.0, 1.0, 0.0);
  
  ...
  
  /* 回転 */
  glMultMatrixd(rt);
  
  ...
  
  /* 描画 */
  glBegin(...);
  ...
  glEnd();
  
  ...
}

• マウスで図形を回転するプログラム