床井研究室

■ 2005年08月26日 [OpenGL][テクスチャ] 第２４回バンプマッピング

2006年09月23日 14:36更新

dot3 バンプマッピング

バンプマッピングは，陰影計算に用いる物体表面の法線ベクトルをテクスチャによって「揺らす」ことによって，物体表面に凹凸が付いたような陰影を得る手法です．

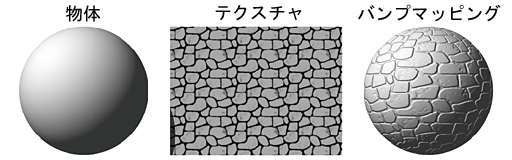
この処理を実現するためには，画素単位に陰影計算を実行する必要があります．ところが OpenGL では，基本的には陰影を頂点単位に求め，面内部の個々の画素の陰影は頂点の陰影を補間して求める手法（グーローシェーディング）が用いられています．このため，この方法ではバンプマッピングを実装できません．

しかしマルチテクスチャなどの機能の追加により，重ねて貼付けた複数のテクスチャの間で，加算などの画素単位の演算を行うことが可能になりました．陰影の拡散反射成分は光線ベクトルと面の法線ベクトルの内積で求めることができますから，この画素単位の演算に内積が用意されていれば，画素単位に陰影付けを行うことが可能になる気がします．OpenGL 1.3 で標準機能となった GL_DOT3_RGB というテクスチャ環境は，２つのテクスチャの間でこの内積計算を実行します．

ということで，今回はこの機能を使ったサンプルプログラムの解説をします．

GL_DOT3_RGB と GL_DOT3_RGBA

内積はベクトル間の演算ですから，テクスチャ間で内積計算を行うには，テクスチャメモリの内容を色ではなくベクトルとして取り扱う必要があります．つまり，テクスチャの R, G, B の各要素を，それぞれベクトルの要素 x, y, z として扱います．その際，単位ベクトルの各要素は -1〜1 の値の範囲を取り得るので，これをテクスチャメモリに格納できる 0〜1 の値の範囲に収める必要があります．このため，単位ベクトルの一つの要素の値 v に対して 0.5v + 0.5 という変換を，あらかじめ行っておきます．

GL_DOT3_RGB あるいは GL_DOT3_RGBA による内積計算は，テクスチャメモリに格納されている単位ベクトルに対して，この変換が行われていることを考慮します．したがって，これらによる画素の内積計算は，２つのテクスチャ a_0{r,g,b} と a_1{r,g,b} に対して，次式により行われます．

この結果の c は，GL_DOT3_RGB の場合は RGB の各要素の値として出力され，GL_DOT3_RGBA の場合は RGBA の各要素の値として出力されます（したがって結果はモノクロ画像として得られます）．

なお，GL_DOT3_RGB によるテクスチャの演算を行うには，GL_TEXTURE_ENV_MODE に GL_COMBINE を指定して，GL_COMBINE_RGB に GL_DOT3_RGB を指定します．

・・・
  
  /* テクスチャユニット１のテクスチャ環境 */
  glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_COMBINE);
  glTexEnvi(GL_TEXTURE_ENV, GL_COMBINE_RGB, GL_DOT3_RGB);
  glTexEnvi(GL_TEXTURE_ENV, GL_SOURCE0_RGB, GL_PREVIOUS);
  glTexEnvi(GL_TEXTURE_ENV, GL_SOURCE1_RGB, GL_TEXTURE);
  
・・・

これにより下地のテクスチャ（GL_PREVIOUS, テクスチャユニット０の出力）と現在のテクスチャ（GL_TEXTURE, テクスチャユニット１が保持するテクスチャ）の内積計算の結果が，テクスチャユニット１の出力になります．下図にこの処理の概略を示します．「高さマップ」，「法線マップ」，および「正規化マップ」については後述します．

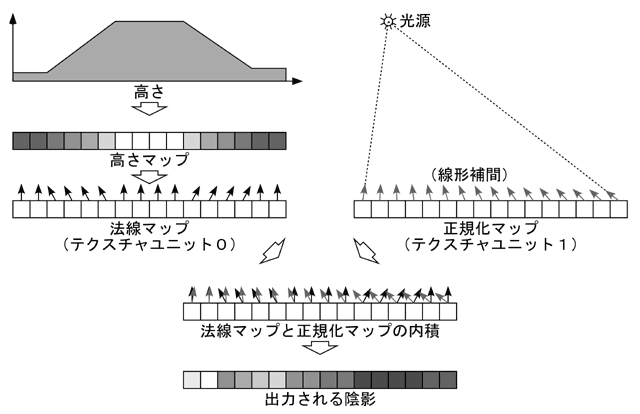
法線マップの作成

個々の画素の値に色ではなく法線ベクトルを格納しているテクスチャのことを，法線マップ（ノーマルマップ）と呼びます．法線マップとなる画像は，あらかじめ作成しておくこともできます（法線マップを作成する GIMP のプラグインや Photoshop のプラグインがあります）が，ここでは高さをグレースケールで表した高さマップ（ハイトマップ）から法線マップを作成してみることにします（ファイル normalmap.cpp）．

・・・
 
/*
** 高さマップをもとに法線マップを作成する
*/
void makeNormalMap(GLubyte *tex, int width, int height, double nz, const char *name)
{
  FILE *fp = fopen(name, "rb");
  
  if (fp) {
    unsigned long size = width * height;
    unsigned char *map = (unsigned char *)malloc(size);
    
    if (map) {
      
      /* 高さマップを読み込む */
      fread(map, height, width, fp);
      fclose(fp);
      
      for (unsigned long y = 0; y < size; y += width) {
        for (int x = 0; x < width; ++x) {
          /* 隣接する画素との値の差を法線ベクトルの成分に用いる */
          double nx = map[y + x] - map[y + (x + 1) % width];
          double ny = map[y + x] - map[(y + width) % size + x];
          /* 法線ベクトルの長さを求めておく */
          double nl = sqrt(nx * nx + ny * ny + nz * nz);
          
          *(tex++) = (GLubyte)(nx * 127.5 / nl + 127.5);
          *(tex++) = (GLubyte)(ny * 127.5 / nl + 127.5);
          *(tex++) = (GLubyte)(nz * 127.5 / nl + 127.5);
          *(tex++) = 255;
        }
      }
      
      free(map);
    }
  }
}

これは実は非常に手を抜いたやり方で，まじめに高さマップの勾配を求めたりせずに，隣接する画素の値の差をそのままベクトルの (x, y) 成分に使っています．したがってこの法線マップは，xy 平面を基準にしたものになります．引数 nz はこのベクトルの z 成分（高さ）なので，この値が大きいほど相対的に x, y 成分が小さくなりますから，ベクトルの振れは少なくなります（平坦に近づきます）．

正規化マップの作成

バンプマッピングを行う際は，法線マップの各画素と光線ベクトルの内積を求めますが，マルチテクスチャ機能を使ってこれを実現する場合は，光線ベクトルもテクスチャである必要があります．そこでポリゴンの頂点における光線ベクトルをテクスチャ座標に用い，キューブマッピングによって正規化された光線ベクトルのテクスチャを得ます．

キューブマッピングでは原点からテクスチャ座標に向かう方向にあるテクスチャがサンプリングされますから，そのテクスチャの各画素に原点からその画素に向かう単位ベクトルを格納しておけば，テクスチャ座標として与えたベクトルを正規化することができます（ファイル normalizemap.cpp）．したがって，これを正規化マップと呼ぶことにします．

・・・
 
/*
** 方向ベクトルをテクスチャ値に変換する
*/
static void vec2tex(float nx, float ny, float nz, GLubyte tex[]) 
{
  tex[0] = (GLubyte)(nx * 127.5 + 127.5);
  tex[1] = (GLubyte)(ny * 127.5 + 127.5);
  tex[2] = (GLubyte)(nz * 127.5 + 127.5);
  tex[3] = 255;
}
 
/*
** 正規化マップの作成
*/
void makeNormalizeMap(GLubyte *tex[], int width, int height)
{
  int i = 0;
  
  for (int v = 0; v < height; ++v) {
    float y = (float)(v + v - height) / (float)height;
    float y2 = y * y;
    
    for (int u = 0; u < width; ++u) {
      float x = (float)(u + u - width) / (float)width;
      float x2 = x * x;
      
      /* 方向ベクトル */
      float r = 1.0f / sqrtf(x2 + y2 + 1.0f);
      float s = x * r;
      float t = y * r;
      
      /* ６面のテクスチャについて方向ベクトルを格納する */
      vec2tex(-r, -t,  s, tex[0] + i);  /* negative x */
      vec2tex( s, -r, -t, tex[1] + i);  /* negative y */
      vec2tex(-s, -t, -r, tex[2] + i);  /* negative z */
      vec2tex( r, -t, -s, tex[3] + i);  /* positive x */
      vec2tex( s,  r,  t, tex[4] + i);  /* positive y */
      vec2tex( s, -t,  r, tex[5] + i);  /* positive z */
      
      i += 4;
    }
  }
}

マルチテクスチャによる合成

後は，このテクスチャをマルチテクスチャによって合成してレンダリングします．まず，テクスチャユニット０（デフォルトのテクスチャユニット）に法線マップを割り当て，通常の２次元マッピングを行います．

・・・
 
/*
** 初期化
*/
static void init(void)
{
  ・・・
  
  /*
  ** テクスチャユニット０に法線マップを設定する
  */
  GLubyte texture[TEXHEIGHT * TEXWIDTH * 4];
  
  /* 法線マップの作成 */
  makeNormalMap(texture, TEXWIDTH, TEXHEIGHT, 20.0, "dotbump.raw");
  
  /* テクスチャの割り当て */
  glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, TEXWIDTH, TEXHEIGHT, 0,
    GL_RGBA, GL_UNSIGNED_BYTE, texture);
  
  /* テクスチャを拡大・縮小する方法の指定 */
  glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
  glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
  
  /* テクスチャの繰り返し方法の指定 */
  glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP);
  glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP);
  
  /* テクスチャユニット０のテクスチャ環境 */
  glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_REPLACE);

またテクスチャユニット１には正規化マップを割り当て，キューブマッピングを行います．このテクスチャユニットでは，下地のテクスチャユニットの出力と GL_DOT3_RGB による内積計算を行います．

  /*
  ** テクスチャユニット１正規化マップを設定する
  */
  glActiveTexture(GL_TEXTURE1);
  
  /* テクスチャの読み込みに使う配列 */
  static GLubyte t[6][128 * 128 * 4];
  static GLubyte *normalize[] = { t[0], t[1], t[2], t[3], t[4], t[5] };
  
  /* 正規化マップの作成 */
  makeNormalizeMap(normalize, 128, 128);
  
  for (int i = 0; i < 6; ++i) {
    /* テクスチャのターゲット名 */
    static const int target[] = {
      GL_TEXTURE_CUBE_MAP_NEGATIVE_X,
      GL_TEXTURE_CUBE_MAP_NEGATIVE_Y,
      GL_TEXTURE_CUBE_MAP_NEGATIVE_Z,
      GL_TEXTURE_CUBE_MAP_POSITIVE_X,
      GL_TEXTURE_CUBE_MAP_POSITIVE_Y,
      GL_TEXTURE_CUBE_MAP_POSITIVE_Z,
    };
    
    /* キューブマッピングのテクスチャの割り当て */
    glTexImage2D(target[i], 0, GL_RGBA, 128, 128, 0, 
      GL_RGBA, GL_UNSIGNED_BYTE, normalize[i]);
  }
  
  /* テクスチャを拡大・縮小する方法の指定 */
  glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
  glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
  
  /* テクスチャの繰り返し方法の指定 */
  glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP);
  glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP);
  
  /* テクスチャユニット１のテクスチャ環境 */
  glTexEnvi(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_COMBINE);
  glTexEnvi(GL_TEXTURE_ENV, GL_COMBINE_RGB, GL_DOT3_RGB);
  glTexEnvi(GL_TEXTURE_ENV, GL_SOURCE0_RGB, GL_PREVIOUS);
  glTexEnvi(GL_TEXTURE_ENV, GL_SOURCE1_RGB, GL_TEXTURE);
  
  /* テクスチャユニット０に戻す */
  glActiveTexture(GL_TEXTURE0);
  
  ・・・
}

図形の描画

図形は，プログラムを簡単にするために，ローカル座標系において xy 平面上に貼りついた四角形ポリゴン１枚にします（ファイル rectangle.cpp）．こうすればポリゴンの向きを法線マップの基準と一致させることができます．

・・・
 
/*
** 矩形の描画
*/
void rectangle(double w, double h, const float l[])
{
  /* 頂点の座標値 */
  const GLdouble vertex[4][3] = {
    { -w, -h, 0.0 },
    {  w, -h, 0.0 },
    {  w,  h, 0.0 },
    { -w,  h, 0.0 }
  };
  
  /* 頂点のテクスチャ座標 */
  static const GLdouble texcoord[4][2] = {
    { 0.0, 0.0 }, { 1.0, 0.0 }, { 1.0, 1.0 }, { 0.0, 1.0 }
  };

このポリゴンの向きをモデリング変換によって変更したときは，それに合わせて法線マップに格納されている全ての法線ベクトルの向きを変更する必要があります．しかし，それでは面の向きを変えるたびに法線マップを作り直さなければなりません．そこで，光線ベクトルの方を法線マップを貼り付ける面の空間（接空間）における方向に変換してやります．ここではモデルビュー変換行列の逆行列を用いて，接空間における光線ベクトルを求めます．

  /* 接空間（＝ローカル座標系）における光源位置 */
  double lt[4] = { l[0], l[1], l[2], l[3] };
  /* モデルビュー変換行列の逆行列 */
  double m[16];
  
  /* 現在のモデルビュー変換行列の逆行列を求める */
  glGetDoublev(GL_MODELVIEW_MATRIX, m);
  inverse(m, m);
  
  /* 接空間（＝ローカル座標系）における光源位置を求める */
  transform(lt, m, lt);
  
  /* 平行光線でなければ実座標を求めておく */
  if (lt[3] != 0.0) {
    lt[0] /= lt[3];
    lt[1] /= lt[3];
    lt[2] /= lt[3];
  }

そして面を描画する際に，法線マップのテクスチャ座標と正規化マップのテクスチャ座標を設定します．法線マップのテクスチャ座標は，普通に２次元テクスチャを貼り付ける場合と同じです．一方，正規化マップのテクスチャ座標には，接空間における光線ベクトルを設定します．これでキューブマッピングを行うことによって，正規化された光線ベクトルを正規化マップから取り出すことができます．

  /* 矩形を描く */
  glBegin(GL_QUADS);
  
  for (int i = 0; i < 4; ++i) {
    /* 法線マップのテクスチャ座標を設定する */
    glTexCoord2dv(texcoord[i]);
    
    /* 接空間における光源の方向ベクトルを
       正規化マップのテクスチャ座標に設定する */
    if (lt[3] != 0.0) {
      glMultiTexCoord3d(GL_TEXTURE1,
        lt[0] - vertex[i][0],
        lt[1] - vertex[i][1],
        lt[2] - vertex[i][2]);
    }
    else {
      glMultiTexCoord3d(GL_TEXTURE1, lt[0], lt[1], lt[2]);
    }
    
    /* 対応する頂点座標の指定 */
    glVertex3dv(vertex[i]);
  }
  glEnd();
}

なお，この手法ではバンプマッピングの内積計算により陰影が求められるので，通常の陰影付け (GL_LIGHTING) はオフにしておきます．

実行結果

左が高さマップ，右がレンダリング結果です．

拡散反射率のテクスチャを合成する（main.cpp を main1.cpp に，rectangle.cpp を rectangle1.cpp に置き換える）と，こんな感じになります．これを実行するには，テクスチャユニットがもう一つ（合計三つ）必要になります．

dot3 バンプマッピングって実は面倒？

ここまで書いてきて言うのもなんですが，dot3 バンプマッピングって，なんだかとても面倒くさいですね．モデルの描画の段階に光源が絡んでくるのも，プログラムがすっきりしなくなるので気に入りません．それに，他のデモやサンプルプログラムでは，物体になぜかトーラスを用いているものが多くて，任意の形状に応用したものをあまり見かけません．任意の形状に dot3 バンプマッピングを適用しようとすれば，モデリング時に法線マップを貼り付けた面の接空間もデータとして保持しておく必要があるように思います．これは，やろうと思えばできなくは無いとは思いますが，なんだかとてもめんどくさいような気がします（これを近似的に求める手法もあるようです）．サンプルプログラムでトーラスが使われるのは，この面の接空間を求めるの容易だからでしょうか．

[コメントを投稿する]

■ 2005年08月26日 [OpenGL][テクスチャ] 第２４回 バンプマッピング