床井研究室

球に dot3 バンプマッピング

前回の最後で「dot3 バンプマッピングは面倒」みたいなことを書いたんですが，一応，接空間の算出が容易な球に対してバンプマッピングを行うサンプルを書いてみました．

• Linux 版
• Mac OS X 版
• Windows 版

こんな感じです．

接空間の設定

前回は単一のポリゴンに対して dot3 バンプマッピングを行ったので，ポリゴンをローカル座標系の xy 平面上に置いて，法線マップの座標系をポリゴンの接空間と一致させました．しかし，複数のポリゴンで構成された物体に対して dot3 バンプマッピングを施す場合は，そういう手抜きができません．

そこで今回は，ポリゴンの一つ一つの頂点に，法線マップの貼付け方に合わせて接空間を設定する方法について説明します．例として，ここでは球に対して下図のように法線マップを貼り付ける場合について考えます．この貼り付け方では極点部分がつぶれてしまいますが，そのあたりは大目に見てください．

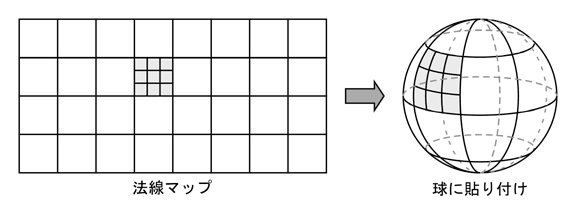
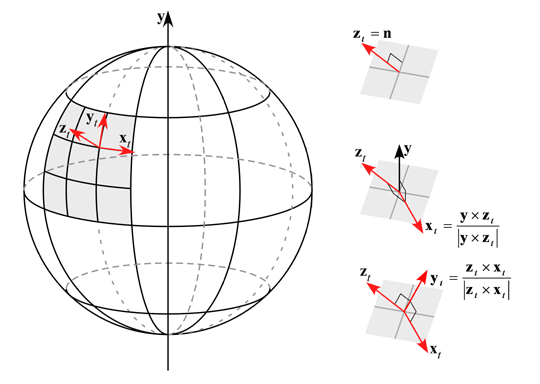
この球面上の一点における接空間は，次のようにして設定します．まず，この点における法線単位ベクトル n を求めます．これをこの接空間の基底ベクトル（軸ベクトル）の z 軸 ( z_t ) に用います．

次に物体の中心軸を y 軸 とし，これと z_t との外積を求め，正規化します．このベクトルはこの点における接線ベクトルになります．これを接空間の基底ベクトルの x 軸 ( x_t ) とします．

最後に z_t と x_t の外積を求めて正規化し，この点における従法線ベクトルを求めます．これを接空間の基底ベクトルの y 軸 ( y_t ) とします．

この手順をプログラムにすると，こんな具合になります（ファイル sphere.cpp）．このプログラムでは光源位置の変換に使う行列（後述）の算出まで行っています．

・・・
 
/*
** ローカル座標系から n を法線ベクトルとする接空間の座標系への変換行列 t を求める
*/
static void localToTangent(const double n[3], double t[16])
{
  double l = n[0] * n[0] + n[2] * n[2];
  double a = sqrt(l);
  
  /* 接空間のＸ軸 = (0, 1, 0) × n */
  if (a > 0) {
    t[ 0] = n[2] / a;
    t[ 8] = -n[0] / a;
  }
  else {
    t[ 0] = 0.0;
    t[ 8] = 0.0;
  }
  t[ 4] = 0.0;
  t[ 3] = 0.0;
  
  /* 接空間のＹ軸 = Ｚ軸 (= n) × Ｘ軸 */
  t[ 1] = -n[1] * n[0];
  t[ 5] = l;
  t[ 9] = -n[1] * n[2];
  a = sqrt(t[ 1] * t[ 1] + t[ 5] * t[ 5] + t[ 9] * t[ 9]);
  if (a > 0) {
    t[ 1] /= a;
    t[ 5] /= a;
    t[ 9] /= a;
  }
  else {
    t[ 1] = 0.0;
    t[ 5] = 0.0;
    t[ 9] = 0.0;
  }
  t[ 7] = 0.0;
  
  /* 接空間のＺ軸 (= n) */
  t[ 2] = n[0];
  t[ 6] = n[1];
  t[10] = n[2];
  t[11] = 0.0;
  
  t[12] = 0.0;
  t[13] = 0.0;
  t[14] = 0.0;
  t[15] = 1.0;
}

接空間における光源位置の算出

接空間の基底ベクトルが求められたら，それから接空間における光源の位置を求める変換行列 T を算出します．これは次式で求められます．前述のプログラムはこの計算も含んでいます．

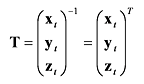
関数 normalizeTexCoord() は，この T を使って接空間における光源位置を求め，それを正規化マップのテクスチャ座標に設定します．

まず，光源が平行光線でなければ，ローカル座標系における光源位置（引数 ll）の実座標を求めておきます．そして，これを T（変数 t）により変換して，この接空間における光源位置を求めます．これをテクスチャ座標に設定します．

/*
** 正規化マップのテクスチャ座標を設定する
** 　n: その点における法線ベクトル
** 　p: その点の位置
** 　ll: ローカル座標系における光源位置
*/
static void normalizeTexCoord(double n[], double p[], double ll[])
{
  /* 接空間における光源位置 */
  double lt[4] = { ll[0], ll[1], ll[2], ll[3] };
  /* ローカル座標系から接空間の座標系への変換行列 */
  double t[16];
  
  /* 平行光線でなければ光源位置の実座標を求めておく */
  if (lt[3] != 0.0) {
    lt[0] = lt[0] / lt[3] - p[0];
    lt[1] = lt[1] / lt[3] - p[1];
    lt[2] = lt[2] / lt[3] - p[2];
  }
  
  /* ローカル座標系から接空間の座標系への変換行列を求める */
  localToTangent(n, t);
  
  /* 接空間における光源位置を求める */
  transform(lt, t, lt);
  
  /* 接空間における光源位置をテクスチャ座標に設定する */
  glMultiTexCoord3dv(GL_TEXTURE1, lt);
}

球の描画

これらを用いて球を描画します．まず，現在のモデルビュー変換行列を取り出し，その逆行列を求めます．これを用いて球のローカル座標系における光源位置（変数 ll）を求めます．

/*
** 球の描画
*/
void sphere(double radius, int slices, int stacks, const float l[])
{
  /* ローカル座標系における光源位置 */
  double ll[4] = { l[0], l[1], l[2], l[3] };
  /* モデルビュー変換行列の逆行列 */
  double m[16];
  
  /* 現在のモデルビュー変換行列の逆行列を求める */
  glGetDoublev(GL_MODELVIEW_MATRIX, m);
  inverse(m, m);
  
  /* ローカル座標系における光源位置を求める */
  transform(ll, m, ll);

この球は円柱の上下をすぼめて作っているので，基本的な描画手順は円柱の場合と変わりありません．また，各頂点の位置を求める際，同時にその頂点における法線ベクトルも算出しておきます．

  /* 球を描く */
  for (int j = 0; j < stacks; ++j) {
    double t0 = (double)j / (double)stacks;
    double t1 = (double)(j + 1) / (double)stacks;
    double r0 = sin(PI * t0);
    double r1 = sin(PI * t1);
    double n[2][3], p[2][3];
    
    /* 法線単位ベクトルの y 成分 */
    n[0][1] = -cos(PI * t0);
    n[1][1] = -cos(PI * t1);
    
    /* 頂点の y 座標値 */
    p[0][1] = radius * n[0][1];
    p[1][1] = radius * n[1][1];
    
    /* 法線マップのテクスチャ座標の算出 */
    t0 *= 4.0;
    t1 *= 4.0;
    
    glBegin(GL_QUAD_STRIP);
    for (int i = 0; i <= slices; ++i) {
      double s = (double)i / (double)slices;
      double a = -2.0 * PI * s;
      
      /* 法線単位ベクトルの x, z 成分 */
      n[0][0] = r0 * cos(a);
      n[0][2] = r0 * sin(a);
      n[1][0] = r1 * cos(a);
      n[1][2] = r1 * sin(a);
      
      /* 頂点の x, z 座標値 */
      p[0][0] = radius * n[0][0];
      p[0][2] = radius * n[0][2];
      p[1][0] = radius * n[1][0];
      p[1][2] = radius * n[1][2];
      
      /* 法線マップのテクスチャ座標の算出 */
      s *= 8.0;

法線マップのテクスチャ座標には，球を描くために求めた緯度方向のパラメータ（変数 t0, t1）と経度方向のパラメータ（変数 s）をスケーリングしたものを用います．正規化マップのテクスチャ座標は，その頂点の法線ベクトル（変数 n）と位置（変数 p），および球のローカル座標系における光源位置（変数 ll）を用いて，前述の関数 normalizeTexCoord() により設定します．

      /* 法線マップのテクスチャ座標を設定する */
      glTexCoord2d(s, t0);
      
      /* 正規化マップのテクスチャ座標を設定する */
      normalizeTexCoord(n[0], p[0], ll);
      
      /* 頂点位置 */
      glVertex3dv(p[0]);
      
      /* 法線マップのテクスチャ座標を設定する */
      glTexCoord2d(s, t1);
      
      /* 正規化マップのテクスチャ座標を設定する */
      normalizeTexCoord(n[1], p[1], ll);
      
      /* 頂点位置 */
      glVertex3dv(p[1]);
    }
    glEnd();
  }
}