床井研究室

大晦日

なんだかんだ言ってる間に, 大晦日になってしまいました. B4 & M2 の方は, 論文の進捗は具合いかがでしょうか. 研究内容についてはあんまり心配していませんけど, プログラムにこだわって文章書くのが後回しになっていないかが心配です. でも, こういうことを大晦日に書いたりして, 私もしかして鬼？ ところで, 私は昨日の夜, 家族と一緒に「のだめカンタービレ」を見に行ってきました. 結構面白かったです. 焦っている (かも知れない) 学生さんを尻目にお気楽やってる私もしかして鬼？

企画書

ここ読んでる学生さんに質問していいですか？ 演習で企画書を書いてもらったら, かなりの人が PowerPoint でも Word でもなく Illustrator で「描いて」きたんですけど, どうしてそういうことになるんでしょうか. ページものを作るのに 1 ページ 1 ページ Illustrator で描いて Acrobat でまとめたりするのは, すごく骨が折れると思うんですけど. 他の講義の文章しか書いてないレポートでも Illustrator を使っている人がいたんで, 以前から不思議に思ってました.

まあ, 1 ページごとにしっかり作りこんであれば, それも悪くはないと思います. また「パワポ不況 - 麻布論壇」という意見もありますから, 道具が押し付けてくる「流儀」に合わせなきゃなんない理由もありません. でも, 書きたいところに自由にものを配置することは, LaTeX をやったときに説明したと思うけど (覚えてないだろうなー), 実際にはとっても手間がかかる作業です. ワープロや LaTeX なんかは, そういう手間を減らして仕事の能率を上げようっていう道具ですよね (OA - オフィスオートメーションって言うくらいだし). そういうものに乗っからずに自分の思うとおりのことを自由に表現したいってのが, うちの学生さんの気質なのでしょうか. そういや就職活動でも, 推薦をとると束縛されるから自由応募でいきたいという学生さんが結構多いんだけど, この気質と関係あるのかな (関係ないか).

スキニング

やまもんのプログラムをデバッグするかわりにサンプルプログラム書いてやるって約束したけど, いろいろいじっているうちに結局ゲームグラフィックス特論の宿題をシェーダで書き直しただけになってしまったんで, ついでだから冬休みゼミの課題にしてしまいます. うしし. 以下は今回の雛形プログラムです. このプログラムはマウスの右ボタンか左ボタンをドラックすればボーンを動かすことができますが, ボーンしか動きません. 宿題プログラムと同じですね. うしし.

• Linux 版
• Mac OS X 版
• Windows 版

スキニングは Kavan の Dual Quaternions で決まり！ と言い切ってしまうと, こみやーまんの立場が無いんだけど, 体積を (近似的に) 維持できることくらいは売りになるかなぁと思っていたら, 今年の SIGGRAPH ASIA で体積を維持した変形手法に関する発表があったみたいで orz (まだ論文読んでない …でもまた後回し〜). まあ, どうでもいいけど SIGGRAPH ASIA 行きたかったなー行きたかったなー.

ボーンの配置と変形アニメーション

とりあえず, 骨格として使うボーンを定義します. もとのボーンは原点 (0, 0, 0) が根元で (0, 0, 1) が先端になっている線分です. このボーンの形は画面表示するために使うもので, 本質には関係ありません. また, これが z 軸の方向を向いているのにも理由があるんですけど, 細かいこだわりなので割愛します. LightWave でも Layout で何も考えずにボーンを追加すると, こういうボーンができるでしょ. このボーンを平行移動と回転により変形させたい (もとの) 形状の付近に配置します. ただしボーンの長さは, これを拡大縮小で決めてしまうと (私のやり方では) いろいろ都合が悪いので, 単に「長さ」として別に保持しておくことにします.

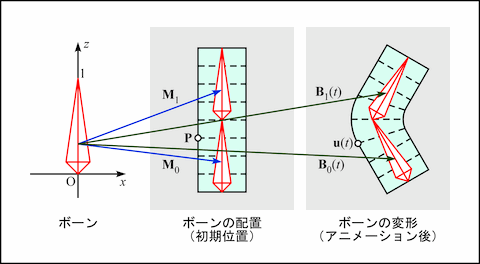
基準位置のボーンを対象形状付近に配置する変換を, それぞれ M₀, M₁ とします. この変換には, 拡大縮小を含まないものとします. ここに拡大縮小を入れてしまうと, 重みの計算が期待通りにできなくなる (拡大したボーンの影響が強くなってしまう) ので, 前述の通りボーン自体の長さを調整して対象形状に合わせます. また, このボーンを時刻 t に応じて変形する変換を B₀(t), B₁(t) とします. こちらの変換には, 拡大縮小も含むことができます. なお B₀(t), B₁(t) は, それぞれ M₀, M₁ からの相対的な変換ではなく, もとのボーンからの絶対的な変換です.

上図のように対象形状の点 P が二つのボーンの影響を受ける場合, 線形和によるバーテックスブレンディングでは, 時刻 t における変形後のその点の位置 u(t) を次式で求めます. ここで w₀, w₁ は, その点がそれぞれのボーンから受ける影響の重みであり, w₀ + w₁ = 1 です.

これは対象形状の点の位置を一旦もとのボーンの座標系に移動し, そこでアニメーションのためにボーンに加えた変換をその点に加えた後, もとの位置に戻すという処理になります. これをその点に影響を与えるすべてのボーンに対して行い, 得られた位置を加重平均して頂点の位置を求めます. 一般に 0〜n - 1 の n 本のボーンの影響を受ける点の位置は, 次式で求めることができます (Real-Time Rendering, Third Edition, P. 83).

(1月4日追記) 以上に対して詳しい説明をいただきましたので, 引用させていただきます. ありがとうございます. 私, 用語をぜんぜん知らないなぁ…

> ボーンを対象形状付近に配置する変換を M0, M1 とします.(中略)
> このボーンを時刻 t に応じて変形する変換を B0(t), B1(t) とします.

一番大事な行列 M と B の定義が馬鹿には解らないのでもう少し解説して欲しい。

M = ボーン（ジョイント）を原点としたジョイント空間からモデル空間への変換行列
M^-1 = その逆行列でモデル空間からジョイント空間への変換
P = モデル空間での頂点の座標とすれば、P' = M^-1 x P が
ジョイント空間での頂点の座標に変換できる。

従ってスキニングは
1. 基本姿勢（バインドポーズ）のモデル空間からジョイント空間に変換 M^-1xP
2. カレントポーズを計算して B = BxBxBx....
3. ジョイント空間からモデル空間に変換 P' = BxM^-1xP
となる。

BxM^-1はフレームの最初に計算しておけるので、ボーンの数だけ全部計算して保存しておく（＝マトリックスパレット）。
あとはこれをGPUに送ってやれば、基本姿勢の頂点座標に行列一発かけるだけでアニメーション後の頂点座標になる。

ボーンのクラス

バーテックスブレンディングの式自体はとっても簡単なんですが, 実装の際にはいろいろ考えないといけないことがあります. まず B_i(t) は, もとのボーンの座標系からの絶対的な変換である必要がありますが, プログラムの実装上は対象形状付近に配置したボーンに対してアニメーションを定義することになると思います. すなわち, ボーンに定義する変換 B'_i(t) は M_i に対する相対的なものであり, B_i(t) = B'_i(t) M_i として B_i(t) を求める必要があります.

さらにボーン同士が親子関係を持つ場合 (だいたい、みなさん、そーされています), 例えば上図において上のボーンが下のボーンに付随して動くような場合には, 上のボーンに定義する変換 M'₁ も M₀ からの相対的なものになりますから, M₁ も M₁ = M'₁ M₀ として求める必要があります. ボーンが枝分かれするなど複雑な階層構造を持っている場合, これをベタに書くとプログラムがぐちゃぐちゃになってしまいそうです.

そこでボーンを (実はやりたくなかったけど) クラスにまとめて, インスタンスごとに局所的な変換を持たせることにします. これにはボーンの初期位置を決める変換 M'_i に用いる回転と平行移動のパラメータ (rotation と position) と, アニメーションを行うために用いる変換行列 B'_i(t) を保持する配列 (animation) を用意します. これに加えてボーンの長さ (length) も保持しておきます (1月4日, ここも参考意見をもとに追加しました).

...
 
class Bone {
  float position[4];    // このボーンを配置する位置 (平行移動成分)
  float rotation[4];    // このボーンを配置する角度 (回転成分)
  float animation[16];  // 配置したボーンに対して加える変形 (アニメーション)
  float length;         // ボーンの長さ (拡大縮小成分)
  const Bone *parent;   // 親のボーンへのポインタ
  ...

ポインタ変数 parent は, そのボーンの親になるボーンを指すのに使います. 根元のボーンには 0 (NULL) を入れておきます. 親のボーンに子供のボーンへのポインタを持たせようとすると可変長の配列なりリストなりを使う必要がでてきてめんどくさいので, 子供の方に親がどれだか教えておきます.

ボーンの描画

ボーンを描画する際に, 現在のボーンから根元のボーンまでの各ボーンの変換を累積した変換行列を求めます. とりあえず現在のボーンの長さを使って, 画面表示するボーンの形状を拡大縮小する変換行列を作成しておきます.

...
 
/*
** ボーンの描画
*/
static void drawBone(const Bone *b, float *bottom, float *top, float *blend)
{
  
  ...
  
  /* ボーンの長さに合わせて拡大縮小する変換行列 */
  Matrix scale;
  scale.loadScale(b->getLength(), b->getLength(), b->getLength());

現在のボーンから parent をたどって根元のボーンに至るまでの各ボーンに設定されている変換を積算していきます. 累積の順序が通常の座標変換と逆順になるので, コードが多少ダサい感じになってます.

  /* ボーンを初期位置に配置する変換行列とアニメーション後の変換行列 */
  Matrix initial, animated;
  initial.loadIdentity();
  animated.loadIdentity();
  
  /* ボーンを根元までたどって各ボーンの変換を累積する */
  do {
    Matrix temp;
    temp.loadTranslate(b->getPosition());  // ボーンを物体付近に移動
    temp.rotate(b->getRotation());         // ボーンを物体に沿わせて回転
    initial = temp * initial;              // M の累積
    temp.multiply(b->getAnimation());      // M * B'(t)
    animated = temp * animated;            // B(t) の累積
  }
  while ((b = b->getParent()) != 0);

累積した変換は, ボーンに対するモデリング変換になります. 最後に, 現在の視野変換に initial と animated をかけて, ボーンに対するモデルビュー変換を求めます.

  /* 現在の視野変換行列をかけておく */
  initial = viewMatrix * initial;
  animated = viewMatrix * animated;

これで initial に各ボーンの初期位置を求める変換, すなわち M_i が格納され, animated に各ボーンのアニメーションの変換を累積したもの, すなわち B_i(t) が格納されます. この initial を使ってボーンの配置後の根元の位置を求め, uniform 変数としてバーテックスシェーダに渡す配列変数 bottom に格納します. 一方, ボーンの先端の位置は initial に先ほど求めた scale をかけたものを使って求め, uniform 変数としてバーテックスシェーダに渡す配列変数 top に格納しておきます.

  /* ボーンの初期位置における根元と先端の位置を求める */
  initial.projection(bottom, boneVertex[0]);
  (initial * scale).projection(top, boneVertex[5]);

アニメーションの変換 animated にボーンの初期位置を求める変換 initial の逆変換をかけます (B_i(t) M^-1_i). この変換は, 対象形状の初期位置における点の位置を, アニメーション後の位置に移動します. これもバーテックシェーダに uniform 変数として渡す変換行列の配列変数 blend に格納しておきます.

  /* バーテックスブレンディング用の変換行列 */
  memcpy(blend, (animated * initial.invert()).get(), sizeof blend[0] * 16);

最後にボーンの形状を描きます. ボーンを指定した長さになるように拡大縮小し, それにアニメーションの変換を加えた後, 投影変換を行います.

  /* attribute 変数 position に頂点情報を対応付けてボーンを描画する */
  glEnableVertexAttribArray(0);
  glVertexAttribPointer(0, 4, GL_FLOAT, GL_FALSE, 0, boneVertex);
  glUniformMatrix4fv(modelViewProjectionMatrixLocation, 1, GL_FALSE, (projectionMatrix * animated * scale).get());
  glDrawElements(GL_LINE_LOOP, sizeof boneEdge / sizeof boneEdge[0], GL_UNSIGNED_INT, boneEdge);
  glDisableVertexAttribArray(0);
}
 
...

点を描く

ボーンの初期位置におけるボーンの根元と先端の位置 (bottom, top), および対象形状の初期位置における点の位置をアニメーション後の位置に移動する変換 (blend) をバーテックスシェーダに渡して, 図形 (点) の描画を行います.

...
 
/*
** 画面表示
*/
static void display(void)
{
  glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
  glEnable(GL_DEPTH_TEST);
  
  /* バーテックスブレンディング用データ */
  GLfloat bottom[BONES][4], top[BONES][4], blend[BONES][16];

まず, drawBone() を使ってボーンの形を描くとともに, bottom, top, および blend を求めます.

  /*
  ** ボーンのアニメーション
  */
  glUseProgram(bProgram);
  
  for (int i = 0; i < BONES; ++i) {
    Matrix animationMatrix;
    animationMatrix.loadRotate(0.0f, 1.0f, 0.0f, angle[i]);
    bone[i].setAnimation(animationMatrix.get());
    drawBone(&bone[i], bottom[i], top[i], blend[i]);
  }

最初に modelViewMatrix に現在の視野変換行列 viewMatrix を格納しておき, それにこの対象形状に対するモデリング変換を適用します. modelViewMatrix にはこの図形に対するモデルビュー変換行列が格納されます. これと現在の投影変換行列 projectionMatrix を uniform 変数としてバーテックスシェーダに渡します.

  /*
  ** 点を描く
  */
  glUseProgram(pProgram);
  
  /* 点のモデリング変換／視野変換／投影変換 */
  Matrix modelViewMatrix = viewMatrix;
  modelViewMatrix.translate(0.0f, 0.0f, -1.5f);
  modelViewMatrix.scale(0.3f, 0.3f, 3.0f);
  glUniformMatrix4fv(modelViewMatrixLocation, 1, GL_FALSE, modelViewMatrix.get());
  glUniformMatrix4fv(projectionMatrixLocation, 1, GL_FALSE, projectionMatrix.get());

またバーテックスブレンディングを行うためのデータとして, 使用するボーンの数 BONES や各ボーンの根元と先端を格納した配列 bottom, top, および対象形状の初期位置における点の位置をアニメーション後の位置に移動する変換行列 blend を, それぞれ uniform 変数 numberOfBones, boneBottom, boneTop, blendMatrix に格納します.

  /* バーテックスブレンディング用の uniform 変数の設定 */
  glUniform1i(numberOfBonesLocation, BONES);
  glUniform4fv(boneBottomLocation, BONES, bottom[0]);
  glUniform4fv(boneTopLocation, BONES, top[0]);
  glUniformMatrix4fv(blendMatrixLocation, BONES, GL_FALSE, blend[0]);

そして点を描きます.

  /* attribute 変数 position に頂点情報を対応付けて図形を描画する */
  glEnableVertexAttribArray(0);
  glBindBuffer(GL_ARRAY_BUFFER, buffer[0]);
  glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, 0);
  glDrawArrays(GL_POINTS, 0, points);
  glBindBuffer(GL_ARRAY_BUFFER, 0);
  glDisableVertexAttribArray(0);
  
  glDisable(GL_DEPTH_TEST);
  glutSwapBuffers();
}

重みの計算

ある点があるボーンから受ける影響の重みは, その点とそのボーンの距離をもとに決定します. これはボーンの両端点のそれぞれと点との距離の和を使うこともできる気がしますが, ここではボーンを通る直線と点との距離を使うことにします. いま, ボーンの根もとの位置を P₀, 先端の位置を P₁ とします. また, 点 P₂ から P₀P₁ を通る直線に下ろした垂線の足を P とします.

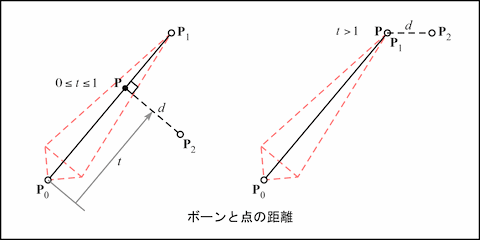
このとき, 線分 P₀P₁ と P₂P は直交するので, 次式が成り立ちます.

点 P は線分 P₀P₁ に対する内分比を t とすれば, 次式で求められます.

これを上式に代入して t を求めます. 高校の数学の復習ですね. でも, これに限らず, うまくコードを書くためには, 公式を持ってくるだけでなく, それを自分なりに噛み砕いておいた方がいいですよ, などと偉そうなこと言ってみたり. 私がうまいコードをかけるわけではないです.

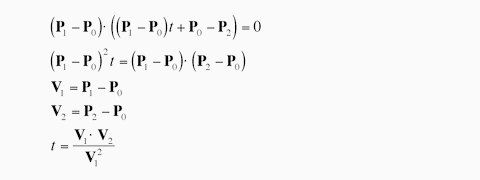
この t を使って, 距離 d を求めます.

ここで V₁= 0 だと t を求めることができませんが, これは線分の長さが 0 (すなわち点) だということなので, d = |V₂| とします. また t < 0 や t > 1 のときは P が P₀P₁ の間にありませんが, t を [0, 1] の区間でクランプしてしまえば, t = 0 のときは d = |V₂| となり, t > 1 のときは d = |P₂ - P₁| となりますから, ボーンの両端点の近い方との距離を得ることができます. 重みはこの距離に 1 を加えたもののベキ乗の逆数を用います. 1 を加えるのは, ( ) 内が必ず 1 以上になるようにするためです.

c を大きくするほど, 近くのボーンの影響力が強まり, 遠くのボーンの影響を受けにくくなります. 逆に c が小さすぎると, ボーンを動かしたときに離れたところの形まで変わってしまうことがあります. LightWave のデフォルトが確か -16 乗くらいになっていたと思うので, とりあえず c = 16 くらいにしておけばいいんじゃないでしょうか.

なお, 位置を同次座標で表している場合は, 重みの総和を求める必要がありません. 同次座標にスカラーをかけても実座標は変わりませんし, このとき同次座標の w の要素にも重みがかけられるので, 重みをかけた同次座標の総和から実座標を求めるための w の要素による除算に, 重みの総和による除算が含まれています. 実はこのことは, 宿題を解答してきた学生さんに指摘されて気づきました.

以上をもとに, 点を描画する際に使うバーテックスシェーダプログラム simple.vert を書き換えて, バーテックスブレンディングにより形状を変形するようにしてください.

• 【解答例】

補足

重みは対象形状とボーンの初期位置との関係で決まるので, 事前に計算しておいて頂点情報 (attribute) として与えるということもできます. しかし, これだとひとつの頂点につきボーンの数 (÷4) だけ頂点情報が必要になるので, ここではバーテックスシェーダ側でその都度計算することにしました. この記事では, 他にも変換行列を積算するのに同じボーンを何度もたどっているなど, 効率の悪い部分があります. ここに書いてあることを鵜呑みにしないで, いろいろいじくってみてください.

あと, この記事では面を張るために必要な法線ベクトルの算出にも触れていません. これは頂点情報に法線ベクトルを与えておいて, その向きをボーンにより変換したものをブレンドすれば求めることがでできると思います. ただし, 法線の変換には法線変換行列 (normal transform matrix) を用いる必要があります. 法線変換行列は頂点位置の変換行列の左上 3x3 要素の随伴行列 (adjoint) を転置したものです. Matrix クラスの normal というメソッドでこれを計算できます (が, 実はまだ使ったことがないので正しいかどうかわかりません). このメソッドで得られたベクトルを正規化してください.

謝辞

2ch の OpenGL 関連のスレッドはとても有益な情報源なので, 時々見ています. 見るたびに, 自分の無知を思い知らされます. 今回の記事の内容は, 本当に以前から学生さんに約束していたことでした (結果的に少し違ってきちゃったのですが). なので「名指し」されたときはさすがにビビリました. ヘタなことは書けなくなったなあと思ったんですが, 学生さん向けの課題なんだから, このスレッドを見なかったことにしても許されるよなとも考えました. 参考になるご意見ありがとうございました.