床井研究室

放射照度マップの作成

前回の記事で説明したとおり, ある方向を向いた面における放射照度は, その面の方向ベクトル (法線ベクトル) と, その方向を天頂とする半天球上の 1 点に向かうベクトルとの内積に, その点における半天球の放射輝度を乗じたものを, 半天球全体について積分 (合計) したものになります.

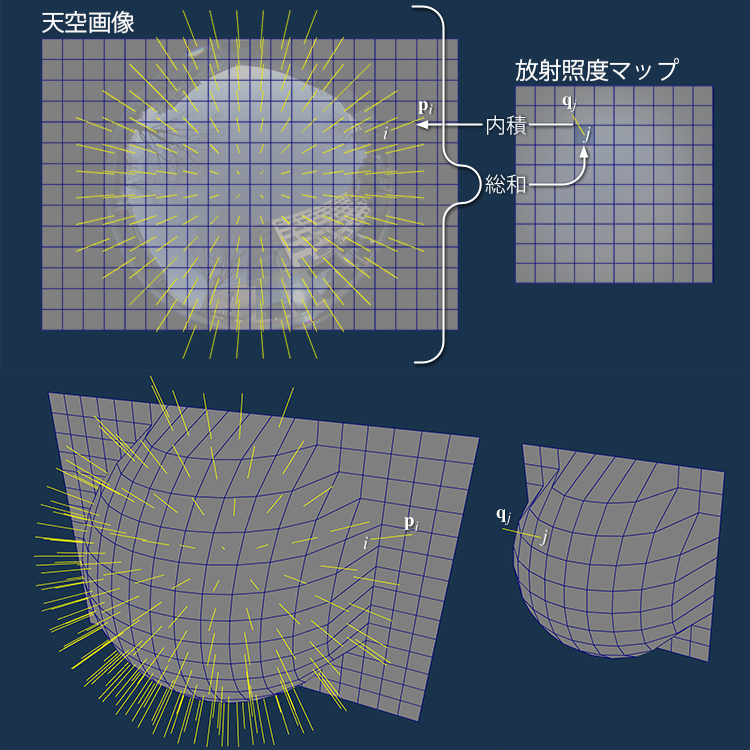
そこで, 放射照度マップに使う画像の個々の画素 j について, その画素において見えている天空の方向 q_j を求めます. 次に, その方向ベクトルと天空画像のそれぞれの画素 i において見えている方向ベクトル p_i との内積に, その画素値 L_i とその画素における天空の立体角 dω_i を乗じます. そして, その値を合計したものを放射照度マップの画素 j の値 E_j とします.

以下は放射照度マップの作成にこの方法を使ったプログラムです.

• 放射照度マッピングによる陰影付けを行ったプログラム

この処理手順*1からわかるように, 放射照度マップの画素値は非常に大きなものになります. ところが古い OpenGL では, このように (ダイナミックレンジの) 大きな値を画素値として取り扱うことができません. そのため, この放射照度マップの値は, OpenGL が取り扱える範囲内にスケーリングする必要があります. この処理により, 陰影計算の物理的な正確さは失われてしまいます.

また, このような積分計算 (畳み込み積分) は, 天空画像や放射照度マップの解像度が高いと非常に大きな計算量になってしまいます. 実際には, こんなに律儀にやらずに間引いて計算しもそれなりに見えますし, 「畳み込み積分」と聞けば「フーリエ変換」などの直交関数解析が使えそうに思えますよね. 球面調和 (Spherical Harmonics, SH) 解析は, まさにそういうものです.

結果を見てもらえばわかりますが, 放射照度マップは非常になだらかな分布になります. したがって放射照度マップに使うテクスチャには, それほど大きな解像度は必要ありません. しかし, それでも各頂点に放射照度マップを持たせることは困難です. また, この手法を使って映り込みのボケを再現 (後述) しようとすると, 輝き係数 (shininess) ごとに異なる映り込みのテクスチャを作成する必要があります.

分布がなだらかであるのなら, それを球面調和解析することにより大幅にデータ量を圧縮できるはずです. 実際, 球面調和解析では, 光源分布を 6 次程度に圧縮します. これなら光源分布を各頂点ごとに持たせることも不可能ではありません. というわけで, プログラマブルな GPU が使える現在では, ここで解説している放射照度マッピングのような手法はあんまり使われません.

天空画像の取得

放射照度マップは全方位画像から作成します. 全方位画像には, 環境マッピングに使うスフィアマップ, キューブマップ, それに二重放物面マップなどのほか, 話題の RICOH THETA や bubi, 360cam, sphericam, SP360 などの全方位カメラで撮影した画像のほか, Panasonic の監視カメラ なんかで撮影した画像が使用できます. でも, 私はそういうカメラを持ってないので (誰か買うてくれ), 陳先生から長いことお借り (パク) してる魚眼レンズ付きの Nikon COOLPIX 995 や, スマホ用の魚眼レンズで撮影した画像を使うことにします.

一方, 放射照度マップの参照にも環境マッピングの手法を用います. スフィアマップは単一の画像で実現できますが, 視点をマップの作成方向から動かすことができません. キューブマップはマップをレンダリングによって作成することが容易ですが, 6 枚の画像をつなぎ合わせて使う必要があり, ちょっと面倒な予感がします. そこで, ここでは 2 枚の画像で実現できる二重放物面マップを作成することにします. また天空画像の場合, 天空の反対側の画像は地面であって, たいていの場合それは一面の地面画像になってしまって, あんまりありがたくない (というのは建前で 2 枚を表裏ぴったり合わせて撮影するのがめんどくさかった) ので, 手を抜いて 1 枚の天空画像だけを使うことにします.

魚眼レンズで取得した天空画像

使用する魚眼レンズは, 角度が画像の中心からの距離に比例する等距離射影方式のものとします. 下図は前述の COOLPIX 995 で撮影した画像です. 太陽が映り込むとスミアが出て具合悪いので, 冬の早朝のまだ太陽の高さが低い時間に撮影しました. でも建物に太陽が映り込んでしまっています. 自分も写りたくないので, 私はカメラにセルフタイマーをセットして地面に置いた後, 建物の陰に隠れています. 朝っぱらから一人で缶蹴りみたいなことしてる自分が情けなかったです*2.

なお, 放射照度マップは, 本当は HDR 画像から作成する必要があります. だから, 本来なら露光量を変えながら複数枚撮って HDR 画像を作るというところから始めんといかんとは思うんですけど, めんどくさいのでしてません. RICOH THETA があれば aimino さんの 360HDR で作れるので, 誰か THETA 買うてください*3.

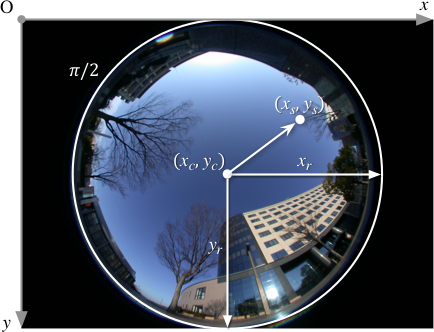
天空画像の各画素における方向ベクトル

この天空画像の各画素について, そこに見えている天空の方向ベクトルを求めます. そのために, まず撮影した画像の画素位置 (x_s, y_s) を, この画像の天空の領域を半径 1 の単位円とする天空画像の座標系上の位置 (s, t) に変換します. ちなみに, この外側は天空画像の反対側, すなわち地面になります. (π の円周部分が真下の 1 点). でも地面の画像は使わないことにしたので, 代わりに大域環境光の強さをこの部分の放射輝度として使ってしまいます.

撮影した画像中の天空の領域の中心の位置を (x_c, y_c) とし, この画像の幅と高さ方向の π / 2 の位置までの長さそれぞれ x_r, y_r としたとき, (s, t) は次式で求めます.

このとき, 天空画像上の点の位置ベクトル (s, t) の長さ r に π / 2 を掛ければ, 撮影位置から天空のこの点に向かうベクトル p = (p_x, p_y, p_z) の天頂角が得られます.

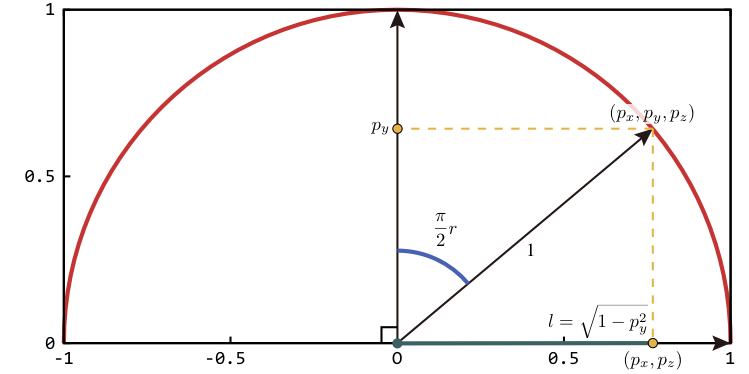
したがって, そのベクトルの y 成分 p_y は次式で求めることができます.

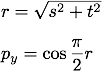
また, この x 成分と z 成分 (p_x, p_z) は, 天空画像上の点の位置ベクトル (u, v) を r で割って正規化したものに, 天空のこの点に向かうベクトルの xz 成分の長さ √ 1 - p_y²  を掛けて得られます.

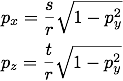
放射照度マップの各画素における方向ベクトル

放射照度マップの参照には, ここでは放物面マッピングの手法を用います. そのため放射照度マップ自体も, これに対応したものを作る必要があります. 放物面マッピングではテクスチャ座標系の半径 0.5 の円内の領域をマッピングしますから, そこに放射照度マップを納めます.

実際には, この外側にも放射照度が存在し, 放射照度マップは中心からなだらかなグラデーションになります. したがって放射照度マップを半径 1 の領域に限定してしまうと, 法線ベクトルの向きによって放射照度が急激に変化して, 不自然な陰影になります. これを避けるには, ちゃんと反対側の放射照度マップを作る (二重放物面マッピングなので) 必要があります*4.

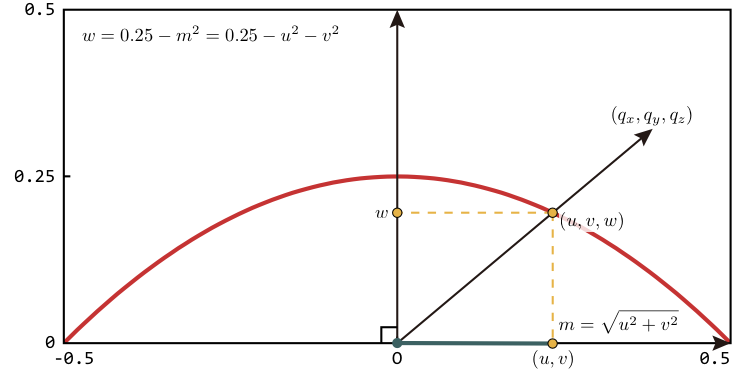
この座標系上の点 (u, v) における放物面マップの方向ベクトル q = (q_x, q_y, q_z) は次式で得られます.

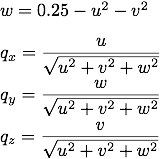
放物面マッピングは, 視線の反射方向 (q_x, q_y, q_z) に見えるものを, テクスチャの (u, v) の位置に格納します (テクスチャを xz 平面に置く場合).

プログラム

冒頭のプログラムの上記の処理の部分を以下に示します. 解説する気力が起きないので, コメントを読んでください. あと結果の放射照度は総和ではなく平均にしているので, π などで割ったりしていません. モデルや手法が間違ってたらごめんなさい.

    // 放射照度マップの各画素について
    for (int yd = 0; yd < size; ++yd)
    {
      ...
      
      for (int xd = 0; xd < size; ++xd)
      {
        // この画素の放射照度マップの配列 dst のインデックス
        const int id((yd * size + xd) * 3);
        
        // この画素の放射照度マップ上の正規化された座標値 (-0.5 ≦ u, v ≦ 0.5)
        const float u(float(xd) / float(size - 1) - 0.5f);
        const float v(0.5f - float(yd) / float(size - 1));
        const float m(u * u + v * v);
        const float w(0.25f - m);
        const float a(sqrt(m + w * w));
        
        // 放射照度マップを放物面マップとして参照するときのこの画素の方向ベクトル q
        const float qx(u / a);
        const float qy(w / a);
        const float qz(v / a);
        
        // この画素が放射照度マップの単位円外にあるとき
        if (qy <= 0.0f)
        {
          // 大域環境光を設定する
          dst[id + 0] = GLubyte(ramb);
          dst[id + 1] = GLubyte(gamb);
          dst[id + 2] = GLubyte(bamb);
          continue;
        }
        
        // このベクトルの方向を天頂とする半天球からの放射照度の総和
        float rsum(0.0f), gsum(0.0f), bsum(0.0f);
        
        // 半天球の重み付け立体角の総和
        float wtotal(0.0f);
        
        // src の (xc, yc) を中心とし [-xr, xr] x [-yr, yr] の範囲の各画素について
        for (int ys = yc - yr; ys <= yc + yr; ++ys)
        {
          for (int xs = xc - xr; xs <= xc + xr; ++xs)
          {
            // この画素の天空画像上の正規化された座標値 (-1 ≦ s, t ≦ 1)
            const float s(float(xs - xc) / float(xr));
            const float t(float(yc - ys) / float(yr));
            
            // この画素の天空画像の中心からの距離
            const float r(sqrt(s * s + t * t));
            
            // この画素の天空画像の中心からの距離を天頂角とする方向ベクトル p の y 成分
            const float py(cos(r * float(M_PI) * 0.5f));
            
            // この画素の天空画像の中心からの距離に対する方向ベクトル q の xz 成分の長さの比
            const float l(r > 0.0f ? sqrt(1.0f - py * py) / r : 0.0f);
            
            // この画素の天空に向かう方向ベクトル q の x 成分と z 成分
            const float px(s * l);
            const float pz(t * l);
            
            // p と q の内積
            const float pq(px * qx + py * qy + pz * qz);
            
            // この画素の方向 p が放射照度マップの方向ベクトル q の反対側を向いているとき
            if (pq <= 0.0f) continue;
            
            // この画素の方向 p の天頂角
            const float theta(acos(pq));
            
            // この画素の方向 p の立体角 (√(1 - cosθ^2) / θ = sinθ / θ = sincθ)
            const float sr(theta > 0.0f ? sqrt(1.0f - pq * pq) / theta : 1.0f);
            
            // この画素の方向 p の立体角に shininess の重みをつける
            const float dw(pow(pq, shi) * sr);
            
            // 重み付け立体角を積算する
            wtotal += dw;
            
            // この画素が天空画像の単位円外にあるとき
            if (r >= 1.0f)
            {
              // 大域環境光を加算する
              rsum += ramb * dw;
              gsum += gamb * dw;
              bsum += bamb * dw;
              continue;
            }
            
            // この画素の天空画像の配列 src のインデックス
            const int is((ys * width + xs) * channels);
            
            // src の画素値を dst に加算する
            rsum += float(src[is + 2]) * dw;
            gsum += float(src[is + 1]) * dw;
            bsum += float(src[is + 0]) * dw;
          }
        }
        
        // 重み付け立体角の総和（天空の面積）で割る
        dst[id + 0] = GLubyte(round(rsum / wtotal));
        dst[id + 1] = GLubyte(round(gsum / wtotal));
        dst[id + 2] = GLubyte(round(bsum / wtotal));
      }
    }

映り込みのテクスチャの作成

上記のプログラムでは, p と q の内積を shi 乗しています. これは, この手続きを映り込みのテクスチャのぼかしににも利用するためです. shi は輝き係数 (shininess) に相当します. 放射照度マップを作成するときは, shi = 1 とします.

映り込みが表面の粗さによってボケる場合は, 微小面モデルにしたがって映り込みのテクスチャをぼかす必要があります. これは Blinn-Phong のモデルによる鏡面反射光の再現と同じです. しかし, この方法はテクスチャのボケの強さが視線ベクトルと法線ベクトルの関係に依存します. つまり, 天空の同じ方向でも, 視線の方向によってボケの量が変化するため, 一つのテクスチャをぼかして使うということができません. そこで, ここではボケの量が視線の方向に依存しない Phong のモデルを使用することにします.

《つづく》