床井研究室

お出かけしたいなあ

これを書いている今日は CEDEC2015 が開催されておりまして, うちの学生さんの中にも参加している人がいます. あっ, この記事, そいつのために書いてるようなもんやないか. くそう今頃気がついた. なんか許せねぇ. SIGGRAPH とか, やっぱり色々お出かけしたいですねぇ. もちろん論文を通して, ですが. がんばろう.

環境による照明

今回は前から気になっていた, 講義のこのあたりの説明をもう一度考え直してみます.

このスライドの説明がグダグダだということもありますけど, これからやろうとしている研究の基礎知識として某学生さんにも押さえておいてほしいことなので, 某学生さんは心して読むように.

1. OpenGL の固定機能による陰影付けを用いたプログラム
2. 放射照度マッピングによる陰影付けを行ったプログラム
3. 放射照度マップをインポータンスサンプリングで作るプログラム

1 は OpenGL の固定機能パイプラインを使って陰影付けを行っている, 元のプログラムです. 2 は 1 に対して放射照度マッピングによる陰影付けを実装したものです. このプログラムでは, OpenGL の固定機能パイプラインによる陰影付けは行っていません. 3 は 2 が放射照度マップの作成に時間がかかりすぎるので, インポータンスサンプリングにより放射照度マップを作るようにしたものです. これは 2 より放射照度マップの画質が落ちます.

放射照度マッピング

放射照度マッピング (Irradiance Mapping) は陰影付け (Shading) をテクスチャマッピングにより行う手法です. このテクスチャを放射照度マップと言い, 映り込みを擬似的に表現する環境マッピングに用いるテクスチャ (環境マップ) から生成することができます.

放射照度マップの生成はレンダリングに先立って行います. したがって, これは事前計算によるレンダリングの高速化手法の一つです. 環境マップに対して事前計算により球面調和 (Spherical Harmonics, SH) 解析を行う事前計算放射輝度伝搬 (Precomputed Radiance Transfer, PRT) などは, この放射照度マッピングから派生 (改良) したものだと言えます.

放射照度マッピングは古い手法ですが, シェーダを使わず, OpenGL のバージョン 1.4 以前の固定機能だけを使って実装することができます.

放射照度とは

放射照度マッピングの説明をする前に, そもそも放射照度とは何かについて簡単に説明します. すでにご存じの話を例によってクドクド説明してしまいますが, こらえてつかあさい.

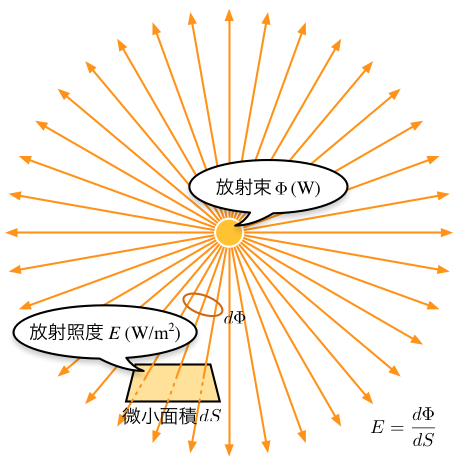
照明が単位時間 (単位: 秒 s) あたりに放出する光のエネルギー (単位: ジュール J) は放射束 (Radiant Flux) といい, 単位はワット (W = J/s) で表されます. なお, 一応補足しますが, これは光源の消費電力ではありません.

この光の一部が空間中のある面積 (単位: m²) の受光面を通過する場合, その単位面積当たりのエネルギーを放射照度といいます. この単位は W/m² で表されます.

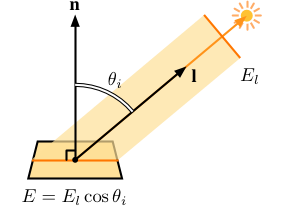
放射照度は単位面積当たりのエネルギーですから, 入射光のエネルギーの総量が一定なら, 照射面積が広いほど放射照度は低下します. 入射光が平行光線なら, 照射面積は入射角の余弦に反比例するため, 放射照度は受光面に対する入射光の入射角の余弦に比例することになります (Lambert の余弦法則).

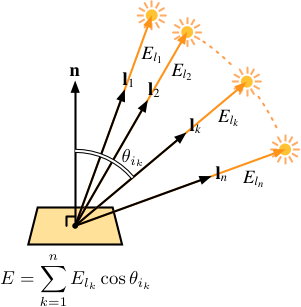
もし光源が複数あれば, 受光面における放射照度は, それらの総和になります.

放射輝度とは

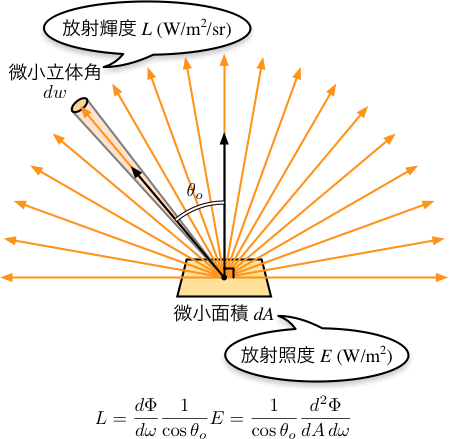
一方, 受光面に入射した光は, 反射により再び空間に放射されます. これを別の方向から観測したとき, その光のエネルギーは観測方向の微小立体角あたりの放射照度になります. これを放射輝度といいます. θ_o 方向から見た受光面 (反射面) の面積は cosθ_o 倍になりますから, この方向に向かう光の放射照度は 1 / cosθ_o 倍になります. これは観測方向から見た受光面 (放射面) 上の一点がどれだけ輝いているかを表します. 放射照度の単位は W/m², 立体角の単位は sr (steradian, ステラジアン) なので, 放射輝度の単位は W/m²/sr になります.

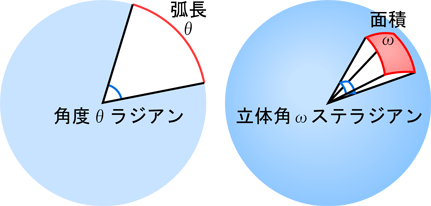
立体角は単位球 (半径 1 の球) の表面上の領域の面積です. 弧度法では, 角度を単位円 (半径 1 の円) の弧長で表します. 単位円の円周長は 2π なので, 360°は弧度法では 2π になります. これと同様に, 単位球の表面積は 4π なので, 単位球全体の立体角は 4π になります.

放射輝度は光の放射面上の一点の明るさ (輝き) を表します. これは放射面の面積には関係ありません. 一方, 放射照度は光の放射面全体から放出される光の量のうち, 受光面の単位面積あたりに到達する量です. 放射輝度が等しければ, その光源によって照明されている受光面の放射照度は, 光源の面積が広いほど大きくなります.

天空の放射照度

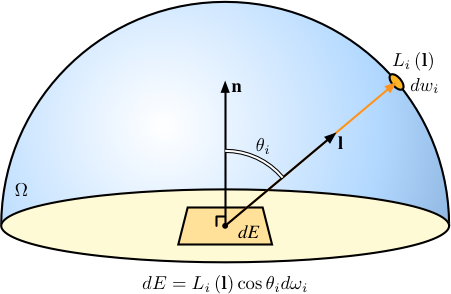
受光面上の一点が, そこから見える天空全体から受ける放射照度について考えます. その点から l の方向にある天空上の一点の放射輝度が L_i(l) のとき, その点からの光による受光面の放射照度は天空上のその点の微小面積を dω_i として L_i(l) cosθ_i dω_i となります.

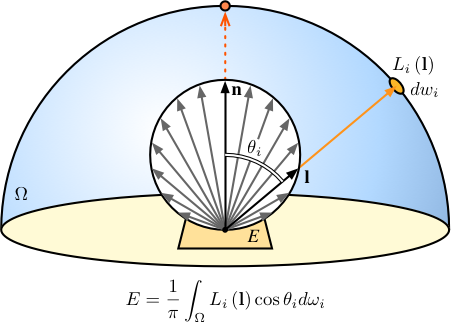
したがって, これを天空の半天球 (Hemi Sphere) Ω について積分すれば, 受光面が天空全体から受ける放射照度 E が得られます. これは受光面の法線方向を中心として, 天空上の一点の放射輝度に入射角の余弦の重みをかけたものの総和です. π で割っているのは, 単位球の半球である半天球により面積 π の単位円の領域が照明される (cosθ_i を Ω について積分すると π になる) からです. ちなみに cosθ_i の「包絡形状」は, 法線方向を軸とした直径 1 の球になります.

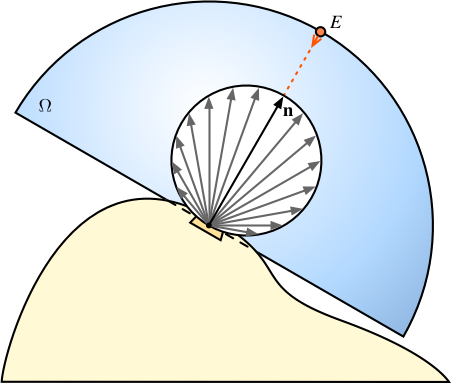
そこで, 天空が無限の彼方 (受光面から十分遠いところ) にあると仮定します. そうすれば, 受光面における放射照度を, その法線だけで決まめることができます. したがって, 天空上の一点を中心として, その周囲の天空の放射輝度に余弦の重みをかけたものの総和を求め, それを天空画像上のその位置の画素に格納した画像をあらかじめ作成しておきます. これが放射照度マップです. レンダリングの際に物体表面の法線ベクトルが向いている位置にあるこの画像の画素の色を使えば, 天空全体を光源とした陰影付けを行うことができます.

これは放射照度マップを物体にテクスチャマッピングし, テクスチャ座標に法線ベクトルを使うことで実現できます.

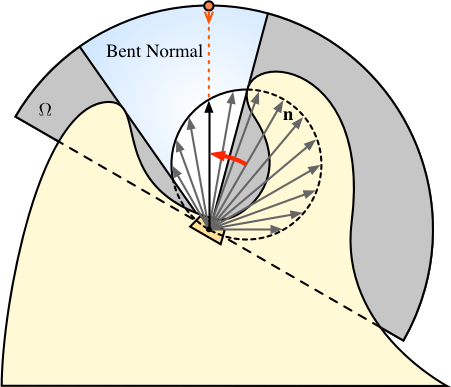
Bent Normal

しかし, このとき受光面が影になっていたりすると, 本来は光が到来するはずのない方向からの光で照明されてしまうことになります. もちろん, これはちゃんと影の処理を行えばよいのですが, 天空は大きな面積をもつ光源ですから, それによる半影をちゃんと計算するのは結構コストの高い処理になります.

そこで, 物体表面の法線ベクトルの方を, あらかじめ天空が見えている方向に傾けておくという手法が採られます. この傾けた法線ベクトルを Bent Normal といいます. これは受光面から天空に向かって直線を何本か伸ばし, そのうち他の物体に遮られずに天空に到達したものの方向ベクトルに対して法線 n に対する余弦を乗じ, それらを平均して求めます.

Ambient Occulusion

なお, このような半影を生成する方法の一つに, Ambient Occulusion があります. これをレンダリング後にスクリーン空間上で求める手法は Screen Space Ambinet Occulusion (SSAO) といいます. このプログラムは魚眼レンズを取り付けたカメラでキャプチャした天空画像をライブで照射照度マッピングし, SSAO や Subsurface Scattering (SSS, 表面下散乱), そして実験的ながら映り込みの遮蔽 (Reflective Occulusion, RO) を再現します. このプログラムで使っている手法はここで解説していますが, 現在モデルを改良しているところです.

《つづく》