床井研究室

大学祭

昨日一昨日はうちの大学祭でして, 「おお, 本学にもリア充は多いのであるな, これらが皆爆発すれば本学は壊滅的な状態になるであろうな」と不穏なことを妄想しつつ和歌山ラーメンをはじめとする屋台の出し物を食い散らかしておりましたところ, うちの学生さんたちのグループの OpenCV 他の技術を応用して作成したインスタレーションの展示に行き当たりました. 学生さんたちがこういう物を作っていたことを全然知らなかったのですが, 自分たちの発想をこういう風に形にしようと思ってくれたことを知って, とても嬉しく思いました. うん, みんながんばれ. 思う存分やってくれ. 作品に頭ぶつけて壊しそうになってすまん.

Crytek の SSAO

えー, ちょっと思うところがありまして, Crytek の SSAO (Screen Space Ambient Occlusion) のアルゴリズムを, Real-Time Rendering (3rd. Ed.) の解説 ("GEMS 本" に手を伸ばす前に, この本とオレンジブックの後半はマジ読んどいたほうがいいです) を参考に自分なりに実装してみました. これは講義で取り上げてはいましたが, 自分では実装したことがありませんでした. ただし, あくまでも自分なりの実装なので, 実際の方法と一致していないと思います. 前述の解説で参照されている文献 Martin Mittring, Finding next gen: CryEngine 2 には, あんまり具体的なことはあまり書いてありませんでした.

この実装で使っている技術的なトピックには, 以下のものがあります.

• マルチテクスチャ
• フレームバッファオブジェクト (FBO)
• マルチプルレンダーターゲット (MRT)
• 浮動小数点テクスチャ

あと，当然ながら遅延レンダリングのテクニックも使います. サンプルプログラムは Mac OS X 10.6 (Snow Leopard) で作成したので想定している OpenGL のバージョンは 2.1 ですが, フレームバッファオブジェクトと浮動小数点テクスチャを使っているので, ビデオカードが GL_EXT_framebuffer_object 拡張機能と GL_ARB_texture_float 拡張機能をサポートしている必要があります. また MRT のターゲットを 4 つ, マルチテクスチャを 7 枚使っています．GeForce 9400M の iMac では動きましたけど, GeForce 7600GS の Linux マシンでは背景しか表示されませんでした.

• サンプルプログラム (11/29 版)

なお, このサンプルプログラムには Xcode 3 のプロジェクトのほか, Linux 用 Makefile と VS2008 のソリューションファイルも付けてあります.

AO (Ambient Occlusion)

サンプルプログラムの解説をする前に, AO (Ambient Occlusion, 環境遮蔽) について少しだけ解説します. このあたりはレンダリングをかじったことのある人にとっては基礎知識ですが, そのうち講義資料にも使うつもりなので, 一応まとめておきます. 光源から物体表面に届く光は, 一般に直接光と間接光に分けられます. レンズを通ってきた光とか鏡に反射した光とかはどうなるなどとややこしいことは, 今は言わないでください.

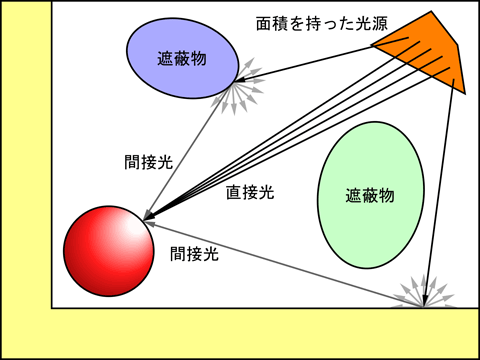
直接光に比べて間接光の経路はとても複雑であり, 場合によっては, ある物体表面での反射光が巡り巡って再び元の物体表面に入射するといった再帰的な経路も含まれていたりします. このため真面目に物体表面に入射する光の量の見積もろうとすると, 結構な手間 (= 処理時間) がかかってしまいます. また, これは反射光を放出するすべての物体表面を光源とみなして処理する必要がありますから, 面積を持った光源を取り扱う必要も出てきます. これもまた面倒な処理になります.

リアルな映像を作成しようと思えば, こういう複雑な光の反射についても手を抜かずに再現する必要があります. しかし時間に限りがあるリアルタイムレンダリングの世界では, 通常こういう複雑な現象をできるだけ単純なモデルで近似して表現しようとします. 伝統的なリアルタイムレンダリングのアプローチでは, 光源は点であるとみなし (omni light), その点からの直接光のみを陰影の発生要因として扱います. このとき間接光はすべての方向から均一の強さで入射するものとして, 定数にまとめてしまいます. これを環境光 (ambient light) と言います.

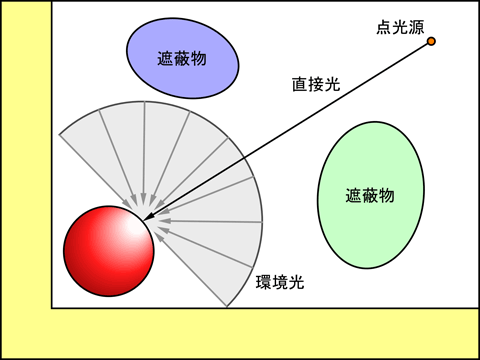
このような近似を行っても一応それらしく見えるので, このモデルは現在でも一般的に用いられています. このモデルは局所照明 (Local Illumination) モデルと言います.

しかし, 入射光のうち直接光以外の成分を定数の環境光にまとめてしまうというのは, 実は結構大胆な近似で, 条件によってはかなり大きな「近似誤差」が知覚されてしまうことがあります．たとえば直接光より間接光が支配的な環境下では, このモデルでは陰影の変化が表現されないために, 生成される画像は平板なものになってしまいます.

一方, 間接光や集光効果, 面積を持った光源などを含む光の振る舞いを精密に表現しようとする場合を, 大域照明 (Global Illumination, GI) モデルと言います. 局所照明モデルは大域照明モデルとの対比において使われる用語です. 大域照明モデルをもとに間接光も手を抜かずに処理すれば, 直接光が届かないところにも陰影の変化が現れます. しかし, このモデルによる映像生成には, 前述のとおり時間がかかります.

大域照明モデルにおいても, いくつかの「近似のレベル」が存在します. 要はどこまで正確にやるかということで, そのレベルはリアリティと速度のトレードオフで決めることになります. そこで間接光を正確に取り扱うことはせず, 物体表面上の一点にどれだけの光が届くかということだけに着目します. このとき光源を均一な明るさの天空全体だとみなせば, その点に届く光の量は, その点から見える天空の割合で決まります. これにより環境光の強さを決定しようとする考え方を, AO (Ambient Occlusion) と言います.

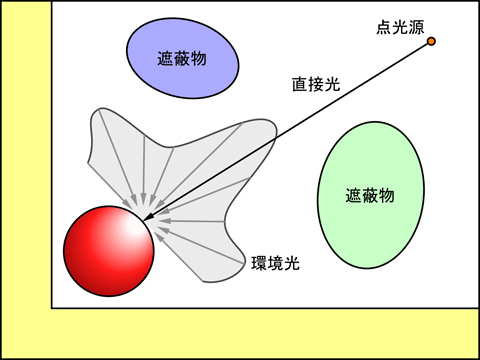
天空全体の明るさが均一であっても, 物体表面上の一点に届く環境光の強さは, 周囲の影響を受けて, その点の位置によって変化します. 光が届きにくい込み入った所は暗くなるというわけです. AO は局所照明モデルに対して, この環境光の不均一さの再現を加えることによって陰影のリアリティを向上しようとする, 大域照明モデルの近似の一つです.

AO の実装

AO の考え方をもとに, 物体表面上の一点 (照射点) における環境光の減衰率 (ここでは環境遮蔽係数と呼ぶことにします) を求める手法には, オブジェクト空間 (object space, ワールド座標系) 中で求める方法とスクリーン空間 (screen space) 中で求める方法があります. オブジェクト空間中で求める方法は, さらに事前計算によって求める方法と, レンダリング時に動的に求める方法があります. 一方スクリーン空間中で求める方法は, レンダリング時に処理するので, これを動的に求めることができます.

AO の実装には様々なものがありますが, オブジェクト空間中で動的に処理する手法としては, Bunnel (NVIDIA) の Dynamic Ambient Occlusion and Indirect Lighting (PDF) が基本のような気がします. 一方, スクリーン空間中で処理する手法には, ここで紹介する Crytek のもののほか, デプスバッファに垂直に放射状に板を差し込む方法 (見覚えがあるんだけど見つからん), デプスバッファにアンシャープマスクをかける Luft (University of Konstanz) らの Image Enhancement by Unsharp Masking the Depth Buffer (PDF), それに McGuire (NVIDIA) の Ambient Occlusion Volumes など, これまたさまざまな方法があります.

まず, 天空を均一の放射輝度 L_A をもつ半球 (hemisphere) だとすれば, N の方向を向いた物体表面上の照射点の位置 P の点における放射照度 E(P, N) は, P, N に関係なく πL_A になります. これが環境光を定数で近似する根拠です. ちなみに, 単位半球面上の入射角 θ 方向の微小面積 (立体角) dω による放射照度は L_A cos θ dω になりますが, cos θ dω は単位半球の底面上の微小面積なので, これを単位半球全体 Ω について積分するということは, 単位半球の底面すなわち単位円内の微小領域を積分することになるので, これは単位円の面積 π になります.

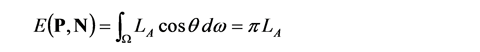
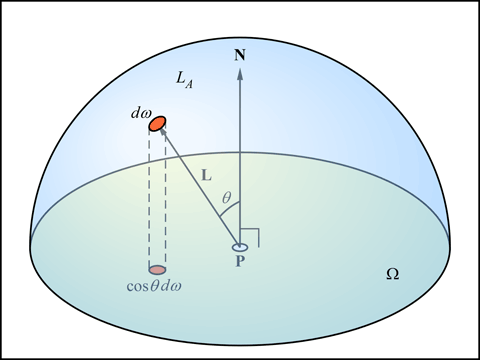
しかし天空と照射点との間に遮蔽物があるとき, 照射点 P から L の方向に遮蔽物があるかどうかを表す関数 (遮蔽関数) を G(P, L) とすれば, E(P, N) は P の関数 k_A(P)πL_A になります. G(P, L) は, L の方向に遮蔽物がなければ 1, あれば 0 となります. この L は Ω について積分するので消えます. この k_A(P) は 0 〜 1 の値を持ちます. これを求める方法を考えます.

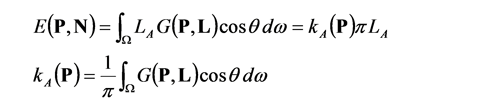
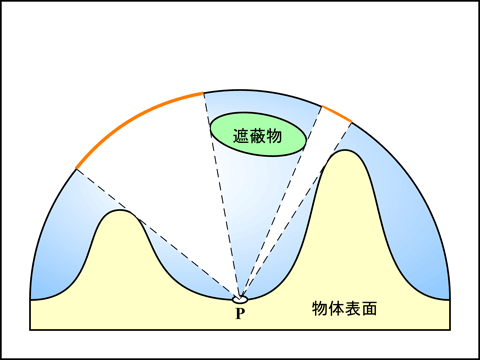
これをレイトレーシング的に求めるなら, 照射点から天空に向けて放射状のレイを飛ばして, 障害物の有無を判定します.

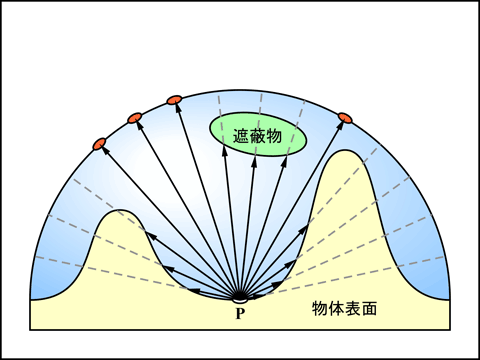
これはオブジェクト空間上で行います. しかしオブジェクトの数が多くなると, この方法では動的に処理することは難しくなるように思われます. これに対してデプスバッファ法による隠面消去処理では, すべての可視オブジェクトの形状が単一のデプスバッファで融合していますから, これを参照すればオブジェクト数に依存せずに処理することができます (表示領域の画素数には依存します). デプスバッファを用いた処理はスクリーン空間で行いますので, このような AO の処理方法を SSAO (Screen Space Ambient Occlusion) と呼びます.

ただしデプスバッファとレイとの交差を求めるのも, またそれなりに手間がかかりそうです. これには恐らく八分木や displacement mapping にも利用されている sphere tracing など, ボクセルに対するレイトレーシングの高速化手法が応用できそうです. デプスバッファに垂直に放射状に板を差し込む方法は, 照射点を頂点とする錐体の形状を求めようとするものです (確認できてないので誤解してるかも知れない). また displecement mapping の手法の一つである relief mapping と同様に, レイ上にいくつかサンプル点を取り, それらとデプスバッファとを比較して, 不可視のものがあれば障害物が存在すると判定することもできます.

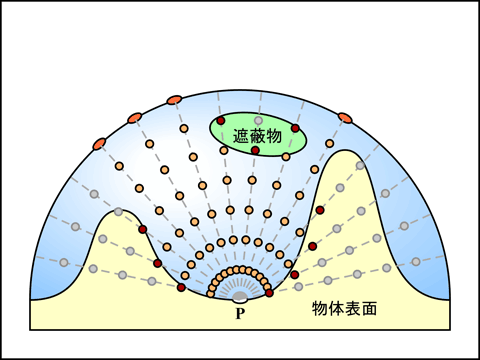
しかし, 最後の方法はあまり速いとは言えないようです. 障害物を見逃さないためにはレイ上に多くのサンプル点をとる必要がありますし, relief mapping とは違ってレイを複数の方向に飛ばす必要があります. 実際やってみたら結構な数のレイを飛ばさないと満足できる品質が得られなくて, サンプル点の数が非常に多くなってしまいました.

Crytek の方法はレイ上にサンプル点をとる代わりに, サンプル点を照射点 P の周囲の球状の領域内にランダムに散布します. そして散布したサンプル点の数の 2 分の 1 に対する, 可視になったものの数の割合を, 点 P における環境遮蔽係数 k_A(P) とします.

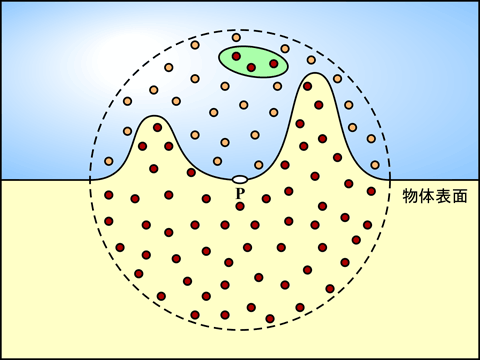
処理の手順

実際の処理の手順を以下に示します.

1. シーンをレンダリングし, 次の画像を生成する.
   • 画素ごとの拡散反射光と鏡面反射光の和 (D + S)
   • 画素ごとの環境光の反射光 (A)
   • 画素位置の可視点の視野空間における座標値 (P)
   • 画素位置の可視点の視野空間における法線ベクトル (N)
2. 各画像をテクスチャメモリに格納する.
3. サンプル点を生成する.
4. シェーダプログラムを有効にする.
5. サンプル点を読み込む.
6. クリッピング空間いっぱいに 1 枚の矩形を描く.

こ手順の 1 の各画像には G バッファ出力に対応した外部の CG ソフトウェアで作成したものを読み込んで使用することもできますが, ここではマルチプルレンダーターゲット (MRT) で構成したフレームバッファオブジェクト (FBO) を使って自前で生成します. あと, AO では多分法線ベクトル (N) は使う必要はないと思うのですが, これがあるとシェーダで色々な効果が実現できるので, ついでに付けておきます.

サンプル点の生成

まずデプスバッファのサンプリングに使う点群を作成します. u を [0, 1) の範囲の一様乱数, v を [-1, 1] の範囲の一様乱数とするとき, 次式で求めた (x, y, z) に点を配置すれば, その点は半径 r の球面上に均一に散らばります.

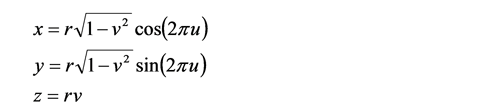
したがって r を次式により求めれば, この点は半径 R の空間中に均一に散布することができます. w は [0, 1] の範囲の一様乱数です.

しかし点群の密度を均一にしてしまうと, 照射点の周囲にある物体の体積を求めることになってしまいます. 遮蔽物の大きさによる影響は照射点からの距離の二乗に反比例するので, 均一だと遠方のものの影響が大きくなり過ぎてしまいます.

密度が距離の二乗に反比例するようにサンプル点を散布すれば, 遮蔽物の影響が距離の二乗に反比例するようになります. そのためには r を次式により求めます. これでも実際に照射点が遮蔽物の影になる割合を求めたことにはなりませんが, 照射点の周りの開口率みたいなものを求めることができるので, これで近似することはできます.

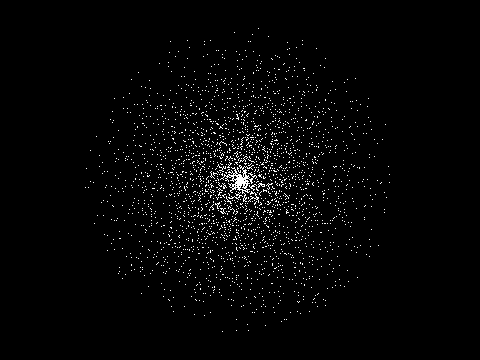
発生した乱数を配列に格納しておき, uniform 変数の配列としてシェーダプログラムに渡します. 最初はこれに浮動小数点テクスチャを使っていたのですが, サンプル点数は高々 200 個くらいなので, uniform 変数で足りると判断しました. テクスチャのサンプリングを行わない分, こちらの方が高速だと思われます.

/*
** 深度のサンプリングに使う点群
*/
#define MAXSAMPLES 256                        // サンプル点の最大数
#define SAMPLERADIUS 0.1f                     // サンプル点の散布半径
static GLfloat pointbuf[MAXSAMPLES][4];       // サンプル点の位置
static GLint point;                           // サンプル点の uniform 変数
 
...
 
/*
** 初期化
*/
static void init(void)
{
  ...
  
  /*
  ** 環境遮蔽係数を算出するのに使う球状の点群
  */
  
  // サンプル点の生成
  for (int i = 0; i < MAXSAMPLES; ++i) {
    float r = SAMPLERADIUS * (float)rand() / (float)RAND_MAX;
    float t = 6.2831853f * (float)rand() / ((float)RAND_MAX + 1.0f);
    float cp = 2.0f * (float)rand() / (float)RAND_MAX - 1.0f;
    float sp = sqrt(1.0f - cp * cp);
    float ct = cos(t), st = sin(t);
    
    pointbuf[i][0] = r * sp * ct;
    pointbuf[i][1] = r * sp * st;
    pointbuf[i][2] = r * cp;
    pointbuf[i][3] = 0.0f;
  }
}

サンプル点の配置

このサンプル点とデプスバッファを比較します. ただし直接比較すると, 陰影が透視補正をしていないテクスチャのように視点の移動に伴ってうにょうにょ動いてしまうことが予想されますので, 一旦これを視野空間上に配置します. そのために処理対象の画素の視野空間上の位置 (P) をテクスチャとして用意しておきます. これには浮動小数点テクスチャを用います.

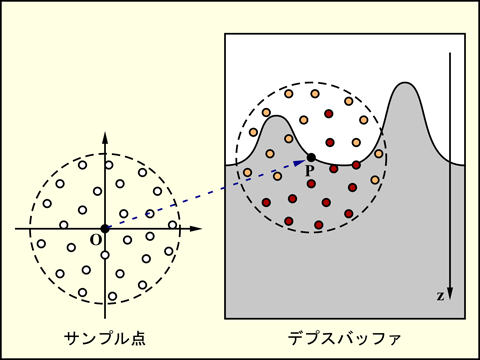
そして配置後のサンプル点の位置を投影変換 (プロジェクション) 行列により座標変換してクリッピング空間上での位置を求めます. これは [-1, 1] の範囲にあるので, テクスチャ空間の [0, 1] の範囲に変換してから, その xy 座標値を使ってデプスバッファをサンプリングし, 取り出したデプス値とサンプル点の z 座標値を比較します.

#version 120
//
// pass2.frag
//
#define MAXSAMPLES 256                  // サンプル点の最大数
 
const int SAMPLES = 256;                // サンプル点数
const float SAMPLING_RATIO = 2.0;       // サンプル点の数の比較係数
 
uniform sampler2D unit[7];              // テクスチャユニット
uniform vec4 point[MAXSAMPLES];         // サンプル点の位置
 
varying vec2 texcoord;
 
void main(void)
{
  ...
  
  // unit[2] から処理対象の画素の視点座標系上の位置 position を取得
  vec4 p = texture2D(unit[2], texcoord);
  
  // 遮蔽されないポイントの数
  int count = 0;
  
  // 個々のサンプル点について
  for (int i = 0; i < SAMPLES; ++i) {
    
    // サンプル点の位置を p からの相対位置に平行移動した後，その点のクリッピング座標系上の位置 q を求める
    vec4 q = gl_ProjectionMatrix * (p + point[i]);
    
    // テクスチャ座標に変換
    q = q * 0.5 / q.w + 0.5;
      
    // q の深度が unit[4] の値 (デプスバッファの値) より小さければ，遮蔽されないポイントとしてカウントする
    if (q.z < texture2D(unit[4], q.xy).z) ++count;
  }
  
  // 遮蔽されないポイントの数から環境遮蔽係数を求める
  float a = clamp(float(count) * SAMPLING_RATIO / float(SAMPLES), 0.0, 1.0);

そして, デプスバッファよりも手前にあるサンプル点の数を数えて, その二倍をすべてのサンプル点の数で割ったものを [0, 1] でクランプします. これをその点の環境遮蔽係数とします. 実は各サンプル点は cos θ の重みを持っているはずなのですけど, 気にしないでも大丈夫！みたいな話になっているようです. サンプル点を 16 にして処理すると, 次のような結果が得られます.

結構ひどい結果になりました. Crytek によれば 200 個程度できれいになるけど, パフォーマンス上は 16 個がせいぜいだそうです. そこで点群を画素位置に応じて切り替えて jittering すれば, こういう結果が得られます.

結構それらしい結果ですが, dithering のような見かけになってしまいました. これは「境界を保った平滑処理で解消できる」とのことですが, 「やってられっかー(ノ`Д´)ノ彡┻━┻」ということで, あきらめてサンプル点を 200 個以上取ることにします. のろいですけど.

余談ですが, jittering の品質を上げるには, より多くの乱数が必要になります. uniform 変数は 4096 個は取れると思ったんですけど, NVIDIA のビデオカードだと 512 個取ろうとしたところで, GLSL のコンパイラ (cgc) がエラー出力にアセンブリコードを出力するという不思議な振る舞いをしてくれました. uniform ではなく浮動小数点テクスチャを使った方がよかったかもしれません.

環境遮蔽係数の適用

求めた環境遮蔽係数を環境光の反射光に適用して, それに拡散反射光と鏡面反射光を合成します. そのために, 拡散反射光と鏡面反射光を加えた画像 (D + S) と, 環境光の反射光の画像 (A) が別々に必要になります. 拡散反射光と鏡面反射光と環境光の反射光を加えた画像は次のようになります.

この環境光の反射光に環境遮蔽係数をかけると, 下のような結果が得られます. 環境光の強度を高めにした方が, AO の効果のありがたみを実感できます.

  // 環境光の反射光 (unit[1]) に環境遮蔽係数を適用
  vec4 color = diffspec + texture2D(unit[1], texcoord) * a;

環境光の反射光と拡散反射光の和に環境遮蔽係数をかけると更に AO の効果が強調されますが, あまり見栄えのいいものになりません. 元の解説にも, 環境遮蔽係数は環境光の反射光のみにかけた方がいいと書いてありました.

背景の追加

クリッピング空間全体に矩形を描いているので, それに画像をマッピングすれば背景になります. 背景と前景を区別するために, 拡散反射光と鏡面反射光の画像のアルファ値を使います.

  // diffspec のアルファ値が 0 なら背景 (unit[6]) のみ
  if (diffspec.a == 0.0) {
    gl_FragColor = texture2D(unit[6], texcoord);
    return;
  }

映り込みの追加

画素ごとに法線ベクトルを得ることができるので, 鏡面球の映り込み画像のテクスチャを法線ベクトルの xy 成分でサンプリングすれば, 映り込みを表現できます.

  // unit[3] から法線ベクトルを取り出す
  vec3 normal = texture2D(unit[3], texcoord).xyz;
  
  // 環境 (反射マッピング)
  color += texture2D(unit[5], normal.xy * 0.5 + 0.5) * reflection;

屈折の追加

同様に, 画素ごとの法線ベクトルを GLSL の組み込み関数 refract() で曲げて, それを使って背景画像をサンプリングすれば, 疑似的な屈折も表現できます. でも, もう疲れてきたので Fresnel の式は実装していません.

  // 背景 (屈折マッピング)
  vec4 bg = texture2D(unit[6], texcoord + refract(vec3(0.0, 0.0, 1.0), normal, refraction).xy * bgdistance);
  
  // 全景と背景を合成して出力
  gl_FragColor = mix(bg, color, color.a);
}

相互反射について

この実装では相互反射については考慮していませんので, AO の効果は必要以上に暗いものになっています. 元の解説では, 相互反射を高速かつ正確に見積もる方法として Stewart (University of Tronto) らの "Toward Accurate Recovery of Shape from Shading Under Diffuse Lighting" (PDF) を紹介しています.

最後に

デプスバッファの内容は奥行き方向に延びているので, この方法で得られる AO の効果は, 奥行き方向に対して不自然なものになる場合があります. これは困ったもんだと思いますけど, SSAO の本質でもあるので, 伝家の宝刀「運用でカバー」を抜くしかないのかもしれません.

おまけ

こんなのとか