«第１７回 レイキャスティング 最新 ゼブラパターンの映り込み»

床井研究室

※このブログは遅くとも 2027 年 3 月に管理者の定年退職により閉鎖します (移転先は管理者本人共々模索中)

■ 2010年01月21日 [OpenGL][GLSL][ゼミ] 第１８回 レイキャスティングふたたび

2010年01月23日 09:56更新

聖子と吉三郎

という少女マンガがありました. 作者は沖倉利津子さんという方です. 先日, ある大学の有名な先生がこのマンガについてつぶやかれまして私はたいそう驚いたのですが, 私もこの時代の少女マンガについては結構熱く語れるんじゃないかと思います. でも, すでにそんなことをしたらとっても恥ずかしい年齢なので, しません. それでこのマンガですが, 中学生の主人公が本屋に CQ 誌を買いに行こうとしたり (このことは後に CQ 誌上でも話題になりました), フォックスハンティングしたり, 彼のリグが私も使っていた TS-600 だったりしたので (中学時代の私の愛機は RJX-601 でしたが), めちゃくちゃつぼにはまりました.

ところで CQ 誌といえば, かつてこの雑誌に手書きの広告を出していた札幌のハムショップが, いまや大手ゲームメーカーですから世の中わかりません. あ, でも Hu-BASIC にはお世話になりました. 当時の他の処理系に比べて緻密で洗練されていたことが広告のイメージと合わなくて, 不可解に感じた記憶があります.

並列性の利用

もう冬休みはとっくに終わってしまったので, 冬休みゼミはこれで最後にします. GPU を計算に利用する最大の動機は, その並列処理の能力にあります. ところが前回の方法では, GPU の並列処理能力をほとんど使っていませんでした. GPU の演算器は複数の画素に対して並列に動作しますが, 前回の方法では 1 画素ずつ順に処理していたため, この並列性が活かされません. そのため演算器の多い上位の GPU を使っても, 処理時間があまり短縮されないということが起こっていました.

またレイトレーシング法では, かつての Links-1 がそうであったように, 視線に対して並列性を活用する方法が一般的だと思います. レイトレーシング法は画像のリアリティの向上に伴って視線の数が指数関数的に増加しますから, レイトレーシング法の利点を活かして高速化しようとすれば, 視線に対して並列性を活用するほうが性能向上の余地が大きいような気がします.

GLSL でこの方法を採用するとき, フラグメントシェーダを一斉に起動するために, 表示領域全体を覆う一枚のポリゴンを描くのが定石です. テクスチャを使って画像処理をする場合でも, そういう方法が使われます. でも実は私, それがなんだか気色悪いんですね. やっぱり素直に CUDA なり OpenCL なりを使うべきだと, こういうプログラムを書くたびにヒシヒシと感じます. ジオメトリシェーダも OpenCL もちゃんと勉強せんといかんなぁ…

最初の視線を生成するための準備

表示領域いっぱいにポリゴンを描くには, クリッピング空間の xy 平面上に -1 ≤ x ≤ 1, -1 ≤ y ≤ 1 の大きさのポリゴンを描きます. このとき, バーテックスシェーダに視点の位置や視野の方向 (に向ける回転の変換行列), および [near, far] の範囲を [0, 1] の範囲に変換する比率を与えて, フラグメントシェーダで視線を生成するための前処理を行っておきます.

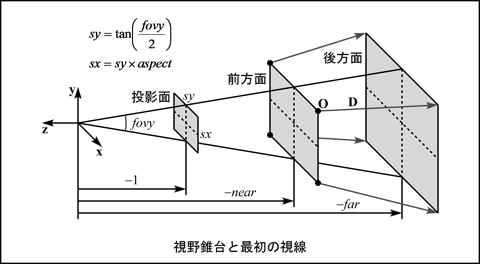
視野錐台と最初の視線

視点から z 軸方向に -1 のところに置いた投影面の大きさを -sx ≤ x ≤ sx, -sy ≤ y ≤ sy とします. 画角を fovy, 表示領域の縦横比を aspect とすれば, sy = tan(fovy / 2), sx = sy × aspect になります.

...
 
/*
** 画面表示
*/
static void display(void)
{
  ...
  
  /* 視点と投影面との距離を 1 としたときの投影面の大きさ */
  GLfloat sy = tan(cameraFov * 0.5f * 3.1415926f / 180.0f);
  GLfloat sx = sy * (float)width / (float)height;

この投影面の -near の位置に置いた前方面への投影像は, 投影面を near 倍したものになります. この投影像上の点が視線の基点になります. これを変数 org に保存しておきます.

  /* 投影面の前方面上の投影像のスケール */
  GLfloat org[3];
  org[2] = cameraNear;
  org[0] = org[2] * sx;
  org[1] = org[2] * sy;

また, この投影面の -far の位置に置いた後方面への投影像の, 前方面上の投影像からの変位は, もとの投影面を far - near 倍したものになります. これは前方面上にある視線の基点から後方面に向かう視線の方向になります. これを変数 dir に格納しておきます.

  /* 投影面の後方面上の投影像の前方面上の投影像からの変位 */
  GLfloat dir[3];
  dir[2] = cameraFar - cameraNear;
  dir[0] = dir[2] * sx;
  dir[1] = dir[2] * sy;

このほか, 視点の位置と目標点の位置から, 視野を回転する変換行列を求めます. これを変数 rot に格納しておきます.

  /* 視線の方向を回転する行列 */
  GLfloat rot[9];
  lookat(cameraPosition, cameraTarget, cameraUp, rot);

シェーダプログラム (バーテックスシェーダ) の uniform 変数にこれらの値を格納します. uniform 変数 cam, org, dir は vec3 のベクトル, rot は mat3 の行列です.

  /* バーテックスシェーダの uniform 変数の場所を得る */
  GLint camLocation = glGetUniformLocation(shader, "cam");
  GLint orgLocation = glGetUniformLocation(shader, "org");
  GLint dirLocation = glGetUniformLocation(shader, "dir");
  GLint rotLocation = glGetUniformLocation(shader, "rot");
  
  /* バーテックスシェーダの uniform 変数に値を設定する */
  glUniform3fv(camLocation, 1, cameraPosition);
  glUniform3fv(orgLocation, 1, org);
  glUniform3fv(dirLocation, 1, dir);
  glUniformMatrix3fv(rotLocation, 1, GL_FALSE, rot);

描画するポリゴンの準備

表示領域全体を覆うポリゴンを, 頂点バッファオブジェクトに転送しておきます. ポリゴンの大きさは xy 平面上で -1 ≤ x ≤ 1, -1 ≤ y ≤ 1 です. これを視線を生成するのにも使うので, 頂点の z 座標値を -1 にしておきます.

  /* 表示領域いっぱいに描くポリゴンの頂点座標 */
  static const GLfloat scr[][3] = {
    { -1.0f, -1.0f, -1.0f },
    {  1.0f, -1.0f, -1.0f },
    {  1.0f,  1.0f, -1.0f },
    { -1.0f,  1.0f, -1.0f },
  };
  
  /* 頂点バッファオブジェクトを生成する */
  GLuint bufferObject;
  glGenBuffers(1, &bufferObject);
  
  /* 頂点バッファオブジェクトにデータを送る */
  glBindBuffer(GL_ARRAY_BUFFER, bufferObject);
  glBufferData(GL_ARRAY_BUFFER, sizeof scr, scr, GL_STATIC_DRAW);
  
  /* attribute 変数の場所を得る */
  GLint scrLocation = glGetAttribLocation(shader, "scr");
  
  /* attribute 変数にバッファオブジェクトの場所を指定する */
  glVertexAttribPointer(scrLocation, sizeof scr[0] / sizeof scr[0][0], GL_FLOAT, GL_FALSE, 0, 0);
  
  /* attribute 変数を有効にする */
  glEnableVertexAttribArray(scrLocation);

ポリゴンの描画

レンダリングする図形のポリゴン (三角形) の頂点の位置や頂点の法線ベクトルは, uniform 変数で与えます. この uniform 変数の場所を求めておいて, 表示領域を覆うポリゴンを描画する関数に渡します.

  /* フラグメントシェーダの uniform 変数の場所を得る */
  GLint posLocation = glGetUniformLocation(shader, "pos");
  GLint vecLocation = glGetUniformLocation(shader, "vec");
  
  /* ポリゴンの描画 */
  obj->draw(posLocation, vecLocation, sizeof scr / sizeof scr[0]);
  
  ...

多数のポリゴンのデータをひとつひとつ uniform 変数を介して GPU に送るのは無駄が多いと思います. たぶん, 形状データを GPU 上のテクスチャメモリあたり (これしか思いつかないけど) にあらかじめ転送しておくといいんでしょう. でも, もう面倒なので uniform 変数で渡してしまいます. 前回の方法では, 形状データをバッファオブジェクトに格納し, 視線を uniform 変数で与えていましたから, 今回の方法は形状データと視線の取り扱い方を入れ替えたことになります.

表示領域を覆うポリゴンを, 形状データを構成する三角形の数だけ描きます. このポリゴンは, シェーダプログラムによって, uniform 変数に指定した三角形の形に切り抜かれます.

...
 
/*
** 図形の表示
*/
void Obj::draw(GLint pos, GLint vec, GLsizei points) const
{
  /* 三角形の数だけポリゴンを描く */
  for (int i = 0; i < nf; ++i) {

なお, pos[0] には P0 を格納しますが, pos[1] には E1 = P1 - P0, pos[2] には E2 = P2 - P0 を格納します.

    int i0 = face[i][0], i1 = face[i][1], i2 = face[i][2];
    
    /* uniform 変数 pos に三角形の頂点 p0 とそこから２頂点に向かうベクトル e1, e2 を格納する */
    GLfloat pos[] = {
      vert[i0][0], vert[i0][1], vert[i0][2],
      vert[i1][0] - vert[i0][0], vert[i1][1] - vert[i0][1], vert[i1][2] - vert[i0][2],
      vert[i2][0] - vert[i0][0], vert[i2][1] - vert[i0][1], vert[i2][2] - vert[i0][2],
    };
    glUniform3fv(posLocation, 3, pos);
    
    /* uniform 変数 vec に三角形の３頂点における法線ベクトルを格納する */
    GLfloat vec[] = {
      norm[i0][0], norm[i0][1], norm[i0][2],
      norm[i1][0], norm[i1][1], norm[i1][2],
      norm[i2][0], norm[i2][1], norm[i2][2],
    };
    glUniform3fv(vecLocation, 3, vec);
    
    /* 表示領域いっぱいに矩形ポリゴンを描く */
    glDrawArrays(GL_TRIANGLE_FAN, 0, points);
  }
}

バーテックスシェーダ

バーテックスシェーダでは描画するポリゴンの頂点座標値 scr に投影面の前方面上でのスケール org をかけます. それを rot により視野の方向に回転して, cam を加えて視点の位置を平行移動します. これは視線の基点 O になります. これを varying 変数 o に代入します. 同様に, scr に投影面の前方面上の投影像から後方面上の投影像への変位をかけて, これも rot により視野の方向に回転します. これは視線の方向 D になります. これを varying 変数 d に格納します.

#version 120
//
// simple.vert
//
uniform vec3 cam, org, dir;
uniform mat3 rot;
attribute vec3 scr;
varying vec3 o, d;
 
void main(void)
{
  o = rot * (org * scr) + cam;
  d = rot * (dir * scr);
  
  gl_Position = vec4(scr, 1.0);
}

描画するポリゴンの各頂点において O と D を求め varying 変数 o, d に代入することにより, これらは補間されてフラグメントシェーダに渡されます. 表示領域全体を覆うポリゴンを描くことによって, 表示領域のすべての画素に補間された O と D が与えられます.

フラグメントシェーダ

フラグメントシェーダでは, 前回同様 Möller らの方法を使って (t, u, v) を求めます. 前回と違うのは, バーテックスシェーダではクリッピング空間の範囲が z 方向についても [-1, 1] だったのに対し, フラグメントシェーダでは gl_FragDepth の値の範囲が [0, 1] になっている点です. このため, 今回の方法では視線の基点を前方面上に設定しています. なお, 以下では t < 0 または t > 1 のときに discard していますが, この判定はなくても問題ないようです. gl_FragDepth がその範囲のフラグメントは捨てられるみたいです.

#version 120
//
// simple.frag
//
uniform vec3 pos[3], vec[3];
varying vec3 o, d;
 
void main(void)
{
  vec3 q = cross(d, pos[2]);
  float s = dot(q, pos[1]);
  
  if (s == 0.0) discard;
  
  vec3 e = o - pos[0]; 
  vec3 r = cross(e, pos[1]);
  float t = dot(r, pos[2]) / s;
  
  if (t < 0.0 || t > 1.0) discard;
  
  float u = dot(q, e) / s;
  float v = dot(r, d) / s;
  float w = 1.0 - u - v;
  
  if (any(lessThan(vec3(u, v, w), vec3(0.0)))) discard;
  
  vec3 n = normalize(w * vec[0] + u * vec[1] + v * vec[2]);
  
  gl_FragColor = vec4(n.z, n.z, n.z, 1.0);
  gl_FragDepth = t;
}

s で割らんで済ます方法ないかな… s 倍したら符号の取り扱いが汚くなりそうだし…

処理時間

あとで計りますけど, こちらのほうが前回のプログラムに対して数十倍速いようです. 特に, 演算器の多い上位の GPU ほど速度の向上率が高くなっています. 演算器 (NVIDIA の場合 CUDA コア) の数が 16 個の GPU で約 10 倍, 64 個の GPU で約 40 倍, 112 個の GPU で約 70 倍でした. 70 / 10 = 112 / 16 = 7, 70 / 40 = 112 / 64 = 1.75 なので, ものの見事に一致しています.

それにしても, こんなに違うもんか… 泣けてくるな (何が).

同僚のコメント

それから前回の記事で「同僚のコメントでへこんだ」みたいなことを書きましたけど, そういうことでへこむのはいつものことなのですぐに復旧しました. 大事なことをちゃんと言ってくれる同僚の皆さんはありがたい存在です. みんな大好きよん♥

[コメントを投稿する]
編集 «第１７回 レイキャスティング 最新 ゼブラパターンの映り込み»
Generated by tDiary version 5.0.14
Powered by Ruby version 3.0.2-p107