床井研究室

気力が…

連休中に無駄な精神エネルギーを費やしてしまったようで, 今週はすこぶる気分が悪いです. そこに私の講義を参観した同僚からシビアなコメントをいただいて (弊社には同僚の講義を参観してコメントするという制度があります) 大きくへこんでいます. 陥没です. 前回の記事も今読み直したらでたらめ書いているように思えます. 後で消そうかな. ああ今日も寒いですね, てゆうかめっちゃ雪降ってるがな. 春早く来んかい私のところに (沢田聖子風).

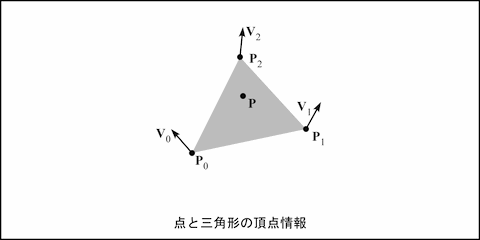
頂点情報

この冬休みゼミでは, なぜだか過去２回続けて点の描画にこだわってきました. 点を描画するには GPU に点の数だけ頂点情報 (attribute) を送ります. この頂点情報には, 普通は座標値やその点における色または法線ベクトル, およびテクスチャ座標などがあります. しかし, 夏休みゼミの第１３回で示したように頂点情報にテクスチャ座標だけを与えて, 座標値や法線ベクトルはバーテックスシェーダで生成するということもできます. 図形の頂点情報として必ずしも座標値を与える必要はなく, 最低限頂点を識別できる情報さえ与えれば, あとはバーテックスシェーダ側で何とでもできたりします.

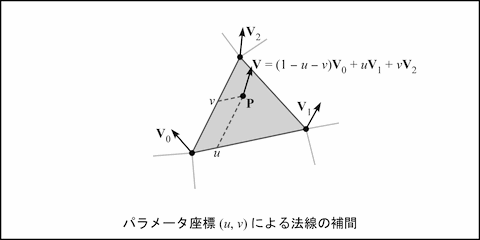
そこで今回は, 一つの点 P を描くために用いる頂点情報として, 三角形の三つの頂点の座標値 P₀, P₁, P₂と, その頂点における法線ベクトル V₀, V₁, V₂ を与えることにします.

レイキャスティング

三角形のデータをもとに点を描く…勘のいい人はもうお分かりですね. そうですね, レイトレーシングですね. ただし, 今回は映り込みや透過・屈折を考えない, 視点から直接放射された第一世代の視線だけについて考えます. いわゆるレイキャスティングです.

レイキャスティングという, OpenGL で採用しているデプスバッファ法とは異なるレンダリングアルゴリズムを, なにも無理して OpenGL の上に実装することはないんです. 素直に CUDA なり OpenCL なりを使ってください. また GLSL もデプスバッファ法を前提に設計されていますから, 他の目的に流用しようとするとどうしても無理や無駄が生じます. 加えてレイトレーシングやレイキャスティングでは, あらかじめ空間分割や階層的な境界箱の設定などを行ってシーンの空間的なコヒーレンシ (一貫性) を抽出しておかなければ, 実用的な処理速度を得ることはできません.

ということで, 今回はかいけーと＋Σくんに参考にしてもらおうと思って書きましたけど, まじで遅い (GeForce 9600GT を使って 17000 ポリゴンくらいのモデルを表示するのに 40 秒くらいかかる) ので全く実用性はありません. 単にシェーダを使えばこういうこともできるという例でしかありませんので, そこんとこよろしく. 次回の方法を参考にしてください.

【ご注意】(←あからさまに外の人向けだな) 以下のプログラムを実行すると, 画面表示が完全に停止したようになることがあります (GeForce 9400M の iMac でなりました). こうなると通常の操作を全く受け付けなくなるので注意してください. また GPU に大きな負担をかけるため, 発熱により GPU を壊してしまうことがあるかも知れません. これについて私は一切責任を負いませんので, ご了承願います. 実行する場合はリセットしても構わないマシンをお使いください. 一方 CPU はほとんど遊んでいるようなので, リモートログインできるようにしておくと吉かも知れません.

• Linux 版
• Mac OS X 版 (走査線ごとに glFinish() したら遅くなったけどハングアップしなくなった)
• Windows 版 (走査線ごとに glFinish() したら遅くなったけど XP でも途中で打ち切られなくなった)

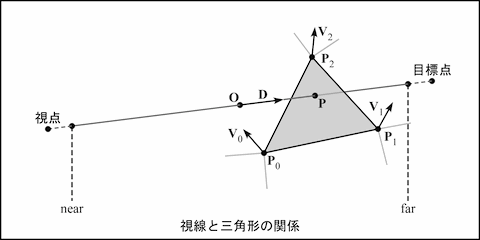
交差判定

交差判定には Möller らによる "Fast, Minimum Storage Ray/Triangle Intersection" の方法を使います. これについては以前に要約を書きました. ただし, ここでは都合により三角形の頂点 V₀, V₁, V₂ を P₀, P₁, P₂ と表します.

いま, 視線の基点を O, 方向を D とします. この視線と三角形との交差の有無と, もし交差する場合はその点の位置を求めます. このとき視線上に交差を求める範囲を設定し, その視点に最も近い位置を near, 最も遠い位置を far とします. この範囲の外にある交差は無視するようにします.

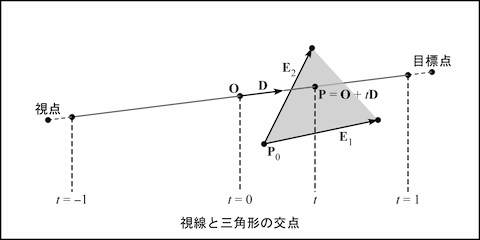
ここで E₁ = P₁ - P₀, E₂ = P₂ - P₀, E = O - P₀, および Q = D × E₂, R = E × E₁ とおいて, 次式により (t, u, v) を求めます.

得られた t は交点 P の視線上の基点 O からの距離になります. これが正かつ最も小さい交点が可視点になります. そこでシーン中のすべての三角形に対して交点を求め, それらの点を GL_POINTS により画面上の同じ位置に重ねて描きます. このとき t を奥行き値に設定してデプスバッファを有効にしておけば, 最終的に視点に最も近い点が残ります. つまり, 画面上の 1 点を描くのにすべての三角形の数だけ点を重ね描きします. むちゃくちゃですね. こんな方法が速いわけありません.

ところで OpenGL では, -1 ≤ x, y, z ≤ 1 の範囲のクリッピング空間内にある図形しか描かれません. そこで視線上の near の位置が -1, far の位置が 1 となるように O と D を設定します. 視点の位置を C とすれば, |D| = (near - far) / 2, O = C + D(1 - near / |D|) となります. OpenGL の場合と異なり, 透視投影の場合でも near = 0 として問題ありません.

一方 u, v は交点 P の三角形上における E₁, E₂ を軸としたパラメータ座標になります.

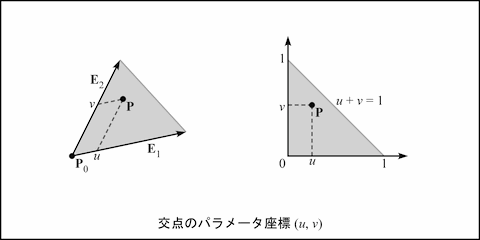
u, v ≥ 0 かつ u + v ≤ 1 のとき, 交点は三角形内にあります. この二つ目の式を変形すれば, 条件を u, v, 1 - u - v ≥ 0 とすることができます.

バーテックスシェーダ

(t, u, v) はバーテックスシェーダで計算します. これらは vec3 でひとつにまとめてしまったほうがいいような気もしますが, 説明がややこしくなるのでそれぞれ float にします. このうち (u, v) を varying としてフラグメントシェーダに送ります. 別に補間するわけではないのに varying というのは気色悪いですが, OpenGL 2.1 / GLSL 1.2 まではそうするしかないので仕方ありません. varying が OpenGL 3.0 / GLSL 1.3 以降で out / in に変更されたのは, こういう理由もあるのかなと思ったりします. 頂点の法線ベクトル V₀, V₁, V₂ も varying 変数の n0, n1, n2 に入れてフラグメントシェーダに送ります.

点の画面上の位置は, uniform 変数 scr に渡すことにします. 視線の基点 O および方向 D は, それぞれ uniform 変数 org と dir に渡すことにします. なお E₁, E₂ は, 頂点情報を頂点バッファオブジェクトに格納する時点で計算しておくものとします.

#version 120
//
// simple.vert
//
uniform vec2 scr;
uniform vec3 org, dir;
attribute vec3 p0, e1, e2;
attribute vec3 v0, v1, v2;
varying float u, v;
varying vec3 n0, n1, n2;
 
void main(void)
{
  vec3 q = cross(dir, e2);
  float s = dot(q, e1);
  float t = -2.0;
  
  if (s != 0.0) {
    vec3 e = org - p0; 
    vec3 r = cross(e, e1);
    
    t = dot(r, e2) / s;
    u = dot(q, e) / s;
    v = dot(r, dir) / s;
    
    n0 = v0;
    n1 = v1;
    n2 = v2;
  }
  
  gl_Position = vec4(scr, t, 1.0);
}

s = 0 のときは視線と三角形が平行なので, このときは交点を持たないこととします. gl_Position に代入する際, scr をその x, y に, t をその z (奥行き) に設定します. t を奥行きに設定することによって, 視線上の [near, far] の範囲外の点がクリッピングにより除外され, 視点に最も近い点がデプスバッファ法による隠面消去処理により選択されます.

フラグメントシェーダ

まず w = 1 - u - v として, (u, v, w) と 0 を比較します. この比較には (速いのかどうか知らないけど) GLSL の組み込み関数 lessThan() を使ってみます. この結果は論理値のベクトル (bvec3) になるので, やはり GLSL の組み込み関数 any() を使っていずれかの要素が真なら discard を呼んでそのフラグメントを捨てるようにします.

#version 120
//
// simple.frag
//
varying float u, v;
varying vec3 n0, n1, n2;
 
void main(void)
{
  float w = 1.0 - u - v;
  if (any(lessThan(vec3(u, v, w), vec3(0.0)))) discard;
  
  vec3 n = normalize(w * n0 + u * n1 + v * n2);
  gl_FragColor = vec4(n.z, n.z, n.z, 1.0);
}

(u, v, w) は頂点情報の補間にも使えます. これで頂点の法線ベクトルを補間します. これと (P = O + tD で求まる) 交点の位置を使って陰影を計算します (t は, フラグメントシェーダでは 2.0 * gl_FragDepth - 1.0 で得ることができます). ここでは力尽きたので, 補間した法線ベクトルの z 値をそのまま陰影に使ってます. この補間はワールド座標系上で行われるので, 透視変換を反映したものになります.

最初の視線の生成

もう力尽きたので, main.cpp の draw() 読んでください. カメラの方向の設定に関して, スクリーンを回転する方法と視線を回転する方法の二つを考えてみましたけど, 本質的に違いはないし, 計算量も変わらないと思います.

あと, O が視線の中間にあると映り込みや屈折を実装するときにややこしいので, O はやはり視線の端にあったほうがいいかもしれません. その場合は |D| = near - far, O = C + D(-near / |D|) として, gl_Position に t を渡すときに 2.0 * t - 1.0 としてください. これはシェーダでやると無駄だし精度が落ちちゃう気が嶋大輔なので, Obj::draw() で調整したほうがいい鴨長明. ああ, もうかなり壊れてきた.

処理時間

以下は Apple iMac (Early 2009) (2.66GHz, GeForce 9400M, 24inch), 画像サイズ 300 × 300 pixels での処理時間です.

うう, ぜんぜん速くない.

エンジニアとクリエータ

前回の記事の最後で「プログラム可能な環境では, そこで何をするのかを決めるのは自分たちだ」みたいな締め方をしてしまったけど, 現実にはすべての開発現場でそういう自由な環境が求められているわけではないと思います. 多くの場合, 出来合いの API を持ってきたほうが効率がいいに決まっています. そう考えると, プログラム可能な環境が一般的になるにつれ, 逆にミドルウェアの役割がこれまで以上に大きくなるかもしれません.

CG 制作にしろゲーム制作にしろ, そういう現場でエンジニアはクリエータ (デザイナ, アニメータ, プランナ，…) という (実は厄介な?) 人たちを相手にしないといけません. でも, そういうところにいるエンジニアは, 実は自分でも CG なりゲームなりを作りたいと密かに思っていたりします. そこでエンジニアは, クリエータの期待に応える仕事をするだけでなく, クリエータを驚かせ, そこから新しい発想を生み出すことのできるような, 魅力的なミドルウェアやツールを作ることで溜飲を下げていたりします (本当か?).

理想論に過ぎないけど, クリエータが消費者の度肝を抜くことを目指し, エンジニアがクリエータの度肝を抜くことを考えているような現場なら, なんかわくわくしてものづくりができそうな気がします. CG やゲームを作ること自体を目標にしなくても, こういうエンジニアの (裏方のようにも見える) 仕事が実はとっても面白いんだということを学生さんに知ってほしいなぁと思うんですけど, どうでしょう. 本当にそういう職場があればですかそうですか.