床井研究室

バージョンアップ

自宅の iMac の OS を Snow Leopard にしました．OS をバージョンアップをすると定常状態に落ち着くまでしばらくかかるんですけど, 今回は更新前と全然変わりなく安定して動いています. いやぁ起動も速いし Firefox もサクサク動くし, Canvas X も Rosetta で一応動きます (日本語の入力ができないけど). あと, このブログを動かしていたマシン (Celeron 1.4GHz, 箱は10年物!) も, 元 M 君マシン (Athlon XP 3200+) に置き換えました. だいぶ軽くなりました. こいつの OS も VineLinux の 5.0 に更新したいんですが, なかなか取りかかれません. tDiary も 2.2.2 に更新したいんですが, なんだかエラーが出るのでちょっとペンディングしています.

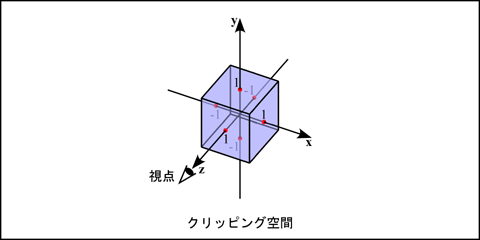
クリッピング空間

レンダリングパイプラインにおいてビューポート変換 (screen mapping) は, -1 ≤ x ≤ 1, -1 ≤ y ≤ 1, -1 ≤ z ≤ 1 の空間の xy 平面への平行投影像を, ディスプレイ上の描画領域 (ビューポート) に写像します. ラスタライザはビューポートからはみ出た図形を描画できませんから, バーテックスシェーダから出力された図形の, この空間からはみ出た部分は, クリッピングにより削り取られます. この空間をクリッピング空間 (canonical view volume) と呼び, この座標系をクリッピング座標系と呼びます.

したがってバーテックスシェーダは, 画面に表示しようとする空間がクリッピング空間に収まるように頂点の位置を座標変換して, gl_Position に出力する必要があります. この変換には, 一般に平行投影 (orthogonal projection) 変換と透視投影 (perspective projection) 変換が用いられます. なお, 平行投影は直交投影とも呼ばれます. また, 透視投影は中心投影とも呼ばれます.

平行投影変換

平行投影変換は, x, y, z のそれぞれの軸に垂直な平面に囲まれた視野空間 (view volume) をクリッピング空間に写像します.

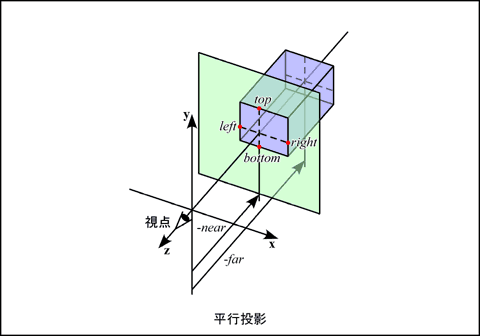
この変換は, x 軸方向について, 視野空間の中心が原点となるように -(right + left) / 2 だけ平行移動し, その大きさを 2 / (right - left) 倍します. y, z 軸についても同様に考えれば, 次の変換行列が得られます.

この変換行列を OpenGL で使用する場合には, ひとつ注意点があります. いま, 行列の各要素 m0〜m15 が次のように並んでいるとします.

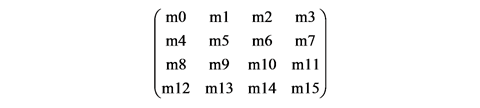
これを OpenGL の座標変換に使う場合, 行列の各要素を次の順序で配列に格納します. つまり変換行列を配列に格納する際は, 行列の要素 m0〜m15 の順序を (見かけ上) 転置しなければなりません.

GLfloat matrix[] = {
  m0,  m4,  m8,  m12,
  m1,  m5,  m9,  m13,
  m2,  m6,  m10, m14,
  m3,  m7,  m11, m15,
};

それでは, left, right, bottom, top, near, far を指定して平行投影変換行列を作成し, 引数 matrix に与えられた配列に格納する関数 orthogonalMatrix() を作成してください.

#include <math.h>
#if defined(WIN32)
#  include "glut.h"
#elif defined(__APPLE__) || defined(MACOSX)
#  include <GLUT/glut.h>
#else
#  include <GL/glut.h>
#endif
 
/*
** 平行投影変換行列を求める
*/
void orthogonalMatrix(float left, float right,
                      float bottom, float top,
                      float near, float far,
                      GLfloat *matrix)
{
  /* この部分を考えましょう */
}

• 【解答例】←考える前に見るなよ

なお, この関数も static 宣言されていない上に最初のほうに "#include" があるということは, ソースファイルは別にしてくれってことだからね.

透視投影変換

透視投影の視野空間は, 原点を頂点とした四角錐を z 軸に垂直な二つの平面 (前方面, 後方面) で切り取った錐台になります. これを視野錐台 (view frustum) と呼びます. 透視投影変換は, この空間をクリッピング空間に写像します.

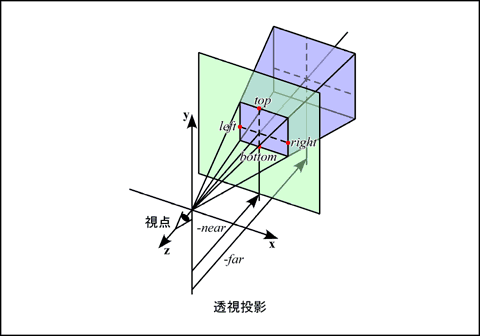
この変換は, 以下の手順で求めることができます. 空間中の点の座標を (px, py, pz) とし, その点が視点から z 方向に -near の位置にある投影面上に投影された位置を (sx, sy) とすれば, sx = -near * px / pz, sy = -near * py / pz になります. また, これらの範囲は left ≤ sx ≤ right, bottom ≤ sy ≤ top なので, これらを -1 ≤ sx', sy' ≤ 1 の範囲に収めるには, sx' = 2 * (sx - left) / (right - left) - 1, sy' = 2 * (sy - bottom) / (top - bottom) - 1 とします. これを整理すると, 次式が得られます.

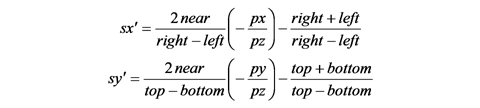
z 軸方向については, (上の図が左手系であることを考慮して) z 軸を反転して, [-near, -far] の範囲を [-1, 1] に写像します. このとき写像後の z 座標値 sz' は, sz の逆数に比例している必要があるので, この関数を sz' = A / sz + B とおきます. sz = -near → sz' = -1, sz = -far → sz' = 1 なので, -1 = A / (-near) + B, 1 = A / (-far) + B となります. これを整理すると, 次式が得られます.

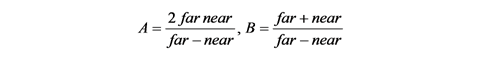
これにより sz' は次式で求めることができます.

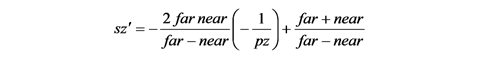
ここで点 (sx', sy', sz') を w = -pz として同次座標で表せば, (-sx' * px, -sy' * pz, -sz' * pz, -pz) となります.

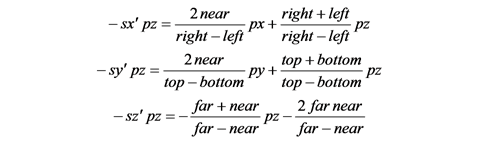
これを行列で表せば, 次の変換行列が得られます.

参考: Eric Lengyel 著, 狩野 智英 訳, "ゲームプログラミングのための 3D グラフィックス数学," pp. 97-99, ボーンデジタル

それでは, left, right, bottom, top, near, far を指定して透視投影変換行列を作成し, 引数 matrix に与えられた配列に格納する関数 perspectiveMatrix() を作成してください.

/*
** 透視投影変換行列を求める
*/
void perspectiveMatrix(float left, float right,
                       float bottom, float top,
                       float near, float far,
                       GLfloat *matrix)
{
  /* この部分を考えましょう */
}

• 【解答例】←これも考える前に見るなよ

この関数も orthogonalMatrix() と同じファイルに書いといてね．

バーテックスシェーダでの座標変換

バーテックスシェーダで座標変換を行うには, 頂点位置が与えられている attribute 変数に変換行列をかけて, gl_Position に代入します. この変換行列や, 光源情報や材質情報などのように, １回の描画単位 (glDrawArrays() や glDrawElements() などの呼び出し) の間に変化しない値は, uniform 変数に格納します. uniform 変数はバーテックスシェーダ, フラグメントシェーダ, およびジオメトリシェーダから共通して参照できる大域変数 （みたいなもの) です.

位置は同次座標 (vec4 型) で計算するので, この変換行列は 4x4 要素である必要があります. このような行列変数は, mat4 型で宣言します. ここではバーテックスシェーダで mat4 型の uniform 変数 projectionMatrix を宣言し, これを用いて attribute 変数 position を座標変換します.

#version 120
//
// simple.vert
//
invariant gl_Position;
attribute vec2 position;
uniform mat4 projectionMatrix;
 
void main(void)
{
  gl_Position = projectionMatrix * vec4(position, 0.0, 1.0);
}

変換行列の uniform 変数への格納

メインプログラムで平行投影変換行列を求め, それを uniform 変数 projectionMatrix に格納します. まず, 前に定義した関数 orthogonalMatrix() の宣言と, 投影変換行列を格納する配列 projectionMatrix の宣言, および uniform 変数 projectionMatrix の場所を記憶する変数 projectionMatrixLocation の宣言を追加します.

...
 
/*
** シェーダオブジェクト
*/
static GLuint vertShader;
static GLuint fragShader;
static GLuint gl2Program;
 
/*
** 投影変換行列
*/
extern void orthogonalMatrix(float left, float right,
                             float bottom, float top,
                             float near, float far,
                             GLfloat *matrix);
static GLfloat projectionMatrix[16];
static GLint projectionMatrixLocation;
 
/*
** attribute 変数 position の頂点バッファオブジェクト
*/
static GLuint buffer;
 
...

次に, 初期化の時点で投影変換行列を求めます. 視野空間は, この図形の右上だけを見ることとして, left = 0, right = 1, bottom = 0, top = 1, near = -1, far = 1 に設定します. また, 同時に uniform 変数 projectionMatrix の場所を探します. uniform 変数が見つからなかったときはエラーなんだけど, いつものごとくエラー処理しとらん.

  ...
  
  /* シェーダプログラムのリンク */
  glLinkProgram(gl2Program);
  glGetProgramiv(gl2Program, GL_LINK_STATUS, &linked);
  printProgramInfoLog(gl2Program);
  if (linked == GL_FALSE) {
    fprintf(stderr, "Link error.\n");
    exit(1);
  }
  
  /* 平行投影変換行列を求める */
  orthogonalMatrix(0.0f, 1.0f, 0.0f, 1.0f, -1.0f, 1.0f, projectionMatrix);
  
  /* uniform 変数 projectionMatrix の場所を得る */
  projectionMatrixLocation = glGetUniformLocation(gl2Program, "projectionMatrix");
  
  /* 頂点バッファオブジェクトを１つ作る */
  glGenBuffers(1, &buffer);
  
  ...

GLint glGetUniformLocation(GLuint program, const GLchar *name);

シェーダプログラムで使われている uniform 変数の場所を探します. program にはシェーダプログラムの名前を指定します. name には uniform 変数の変数名を指定します. 戻り値は uniform 変数の場所です. name に指定した uniform 変数が見つからなければ, これは -1 になります.

そして図形の描画時に, 変換行列の内容を uniform 変数 projectinMatrix に格納します. ここでは glUniformMatrix4fv() の引数 transpose に GL_FALSE を指定して, 配列の内容を転置せずに格納します.

...
 
/*
** 画面表示
*/
static void display(void)
{
  /* 画面クリア */
  glClear(GL_COLOR_BUFFER_BIT);
  
  /* シェーダプログラムを適用する */
  glUseProgram(gl2Program);
  
  /* uniform 変数 projectionMatrix に行列を設定する */
  glUniformMatrix4fv(projectionMatrixLocation, 1, GL_FALSE, projectionMatrix);
  
  /* index が 0 の attribute 変数に頂点情報を対応付ける */
  glEnableVertexAttribArray(0);
  
  ...

void glUniformMatrix4fv(GLint location, GLsizei count, GLboolean transpose, const GLfloat *value);

mat4 型 (4x4 の行列) の uniform 変数に値を格納します. location は glGetUniformLocation() で得られた uniform 変数の場所を指定します. count はデータの個数です. 格納する uniform 変数が配列なら, その要素数までの数が指定できます. 普通の変数なら 1 です. transpose を GL_TRUE にすると引数 value に指定した配列の内容を転置して uniform 変数に格納します. value は uniform 変数に格納するデータの配列です. mat4 型の uniform 変数の要素数は 16 ですから, この配列の要素数は count * 16 個になります.

これで下のような図形が描かれれば OK です.

一応, ここまでのプログラムをまとめたものを, 以下に用意しておきます.

• Linux 版
• Mac OS X 版
• Windows 版