床井研究室

クリッピング空間の奥行き

OpenGL の解説には, しばしば「初期状態では, 視線は Z 軸の負の方向に向いている」と書かれています (私もそう書いてしまいます↓). xy 平面については確かにその通りなんですけど, z 方向についてこれを鵜呑みにすると, 混乱することがあります (私はしました).

クリッピング空間上では, z 軸の正の方向 (視線の反対方向) が奥, 負の方向が手前になります. したがって, クリッピング空間の z = 1 の平面が後方面であり, z = -1 の平面が前方面になります. このためクリッピング座標系上で隠面消去を行うと, 視線方向に対して手前にあるものが, 奥のものに隠されてしまいます. 視野空間を設定する際に near < far とすれば, 頂点の座標値の z 値の符号が反転するので, 奥のものが手前のものに隠されるようになります.

視野変換行列

平行投影変換の次は透視投影変換をやりたいところですが, サンプルのプログラムは図形も視点も xy 平面上にあるので, 視点を動かさないと透視投影変換ができません. なので先に視点の移動を行います.

クリッピング空間では, 視点は原点にあり, 視線は z 軸の負の方向を向いています (^_^;) これを任意の位置から任意の方向を見ることができるようにします. このような変換を視野変換 (viewing transform) と呼びます. いま, 視点が e = (ex, ey, ez) の位置にあり, 目標点 t = (tx, ty, tz) の方向を向いているとします. また視点の「上方向」は u = (ux, uy, uz) とします.

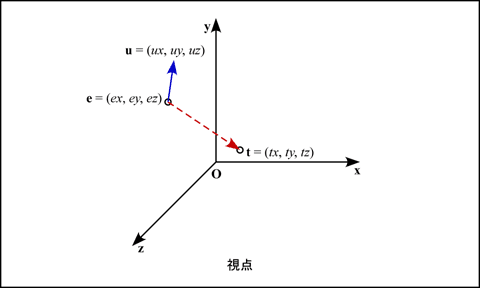
変換行列 T を用いて, この視点が原点になるように平行移動します. e, t は位置なので, これらを同次座標で表せば, それぞれ (ex ey ez 1)^T, (tx ty tz 1)^T となります. これに対して u はベクトルなので, 同次座標は (ux uy uz 0)^T になり, T をかけても変化しません.

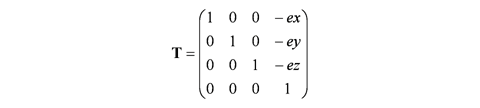
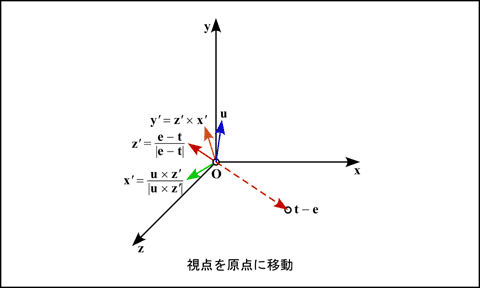
また, 視点座標系の基底ベクトル (軸ベクトル) x', y', z' を求めます. z' は視線の逆ベクトルを正規化して z' = (e - t) / |e - t|, x' は u と z' に対して垂直なので x' = (u × z') / |u × z'|, y' は z' と x' に垂直なので y' = z' × x' となります.

この視点座標系の基底ベクトルが, x, y, z 軸と一致するように回転します.

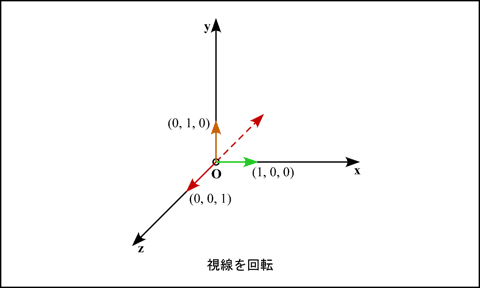
この変換行列 R は, 次のようになります (ううう, 式を間違えた - 9月8日修正). なんでそうなるかは, たとえば x, y, z の各軸ベクトル (1, 0, 0), (0, 1, 0), (0, 0, 1) を, それぞれ (x'_x, x'_y, x'_z), (y'_x, y'_y, y'_z), (z'_x, z'_y, z'_z) に変換する行列を考えてみるとわかります.

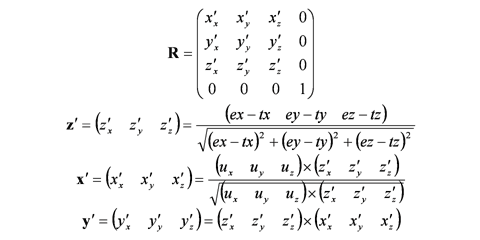
したがって視野変換行列 RT は, 次式により求められます．

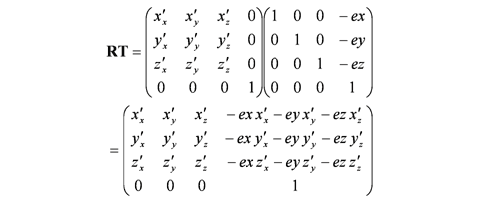
それでは, 視点位置 ex, ey, ez, 目標点位置 tx, ty, tz, 上方向のベクトル ux, uy, uz として視野変換行列を作成し, 引数 matrix に与えられた配列に格納する関数 lookAt() を作成してください.

/*
** 視野変換行列を求める
*/
void lookAt(float ex, float ey, float ez,
            float tx, float ty, float tz,
            float ux, float uy, float uz,
            GLfloat *matrix)
{
  /* この部分を考えましょう */
}

• 【解答例】←すぐに見ちゃだめだってば

この関数も orthogonalMatrix() と同じファイルに書いといてね.

行列の積

視点の移動を行うには, 頂点の座標値に orthogonalMatrix() で作った投影変換行列をかけたものに, lookAt() で作った視野変換行列をかける必要があります. この計算はバーテックスシェーダで行うこともできますが, 先に投影変換行列と視野変換行列の積を求めておけば, バーテックスシェーダの負担を減らすことができます. ４行４列の行列の積は, 次式により求められます.

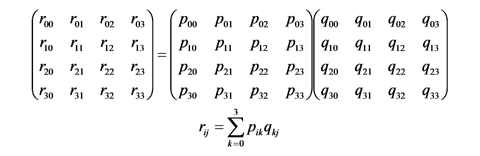
それでは, 引数 m0 に指定された配列に格納されている行列と引数 m1 に指定された配列に格納されている行列の積を求め, 引数 matrix に与えられた配列に格納する関数 multiplyMatrix() を作成してください.

/*
** 行列 m0 と m1 の積を求める
*/
void multiplyMatrix(const GLfloat *m0, const GLfloat *m1, GLfloat *matrix)
{
  /* この部分を考えましょう */
}

• 【解答例】←例としてはあんまり適切ではないかも

ついでだから, この関数も orthogonalMatrix() と同じファイルに書いといてね.

視点の移動

作った関数 lookAt() を使って, 実際に視点を移動します. まず, lookAt() と multiplyMatrix() を呼び出すために, これらの関数の宣言をメインプログラムに追加します.

...
 
/*
** 投影変換行列
*/
extern void orthogonalMatrix(float left, float right,
                             float bottom, float top,
                             float near, float far,
                             GLfloat *matrix);
static GLfloat projectionMatrix[16];
static GLint projectionMatrixLocation;
 
/*
** 視野変換行列
*/
extern void lookAt(float ex, float ey, float ez,
                   float tx, float ty, float tz,
                   float ux, float uy, float uz,
                   GLfloat *matrix);
 
/*
** 行列の積
*/
extern void multiplyMatrix(const GLfloat *m0, const GLfloat *m1, GLfloat *matrix);
 
...

そして, 初期化の段階で視野変換行列を求め, 投影変換行列に掛け合わせます. このために, 視野変換行列を一時的に格納する配列変数 temp0 と, 投影変換行列を一時的に保存しておく配列変数 temp1 を用意しておきます.

...
 
/*
** 初期化
*/
static void init(void)
{
  /* シェーダプログラムのコンパイル／リンク結果を得る変数 */
  GLint compiled, linked;
  
  /* 頂点バッファオブジェクトのメモリを参照するポインタ */
  typedef GLfloat Position[2];
  Position *position;
  
  /* 一時的な変換行列 */
  GLfloat temp0[16], temp1[16];
  
  ...

視野変換行列を temp0 に求めます. 視点の位置は (4, 5, 6), 目標点の位置は (0, 0, 0) にします. また上方向のベクトルは (0, 1, 0) にします.

  ...
  
  /* シェーダプログラムのリンク */
  glLinkProgram(gl2Program);
  glGetProgramiv(gl2Program, GL_LINK_STATUS, &linked);
  printProgramInfoLog(gl2Program);
  if (linked == GL_FALSE) {
    fprintf(stderr, "Link error.\n");
    exit(1);
  }
  
  /* 視野変換行列を求める */
  lookAt(4.0f, 5.0f, 6.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f, temp0);

視野空間は, xy 平面上では -1 ≦ x, y ≦ 1 とします. near と far は, 視点の原点からの距離が約 9 なので, ±2 の範囲をとって, それぞれ 7 と 11 とします. 得られた投影変換行列は temp1 に格納します.

  /* 平行投影変換行列を求める */
  orthogonalMatrix(-1.0f, 1.0f, -1.0f, 1.0f, 7.0f, 11.0f, temp1);

その後，視野変換行列 temp0 と投影変換行列 temp1 をかけて, projectionMatrix に格納します. この projectionMatrix に格納した行列は, uniform 変数 projectionMatrix に渡されます.

  /* 視野変換行列と投影変換行列の積を projectionMatrix に入れる */
  multiplyMatrix(temp0, temp1, projectionMatrix);
  
  /* uniform 変数 projectionMatrix の場所を得る */
  projectionMatrixLocation = glGetUniformLocation(gl2Program, "projectionMatrix");
  
  ...

これで下のような図形が描かれれば OK です.

透視投影変換による描画

それでは, 当初の目的である透視投影変換による描画を行います. まず, 透視投影変換行列を求める関数 perspectiveMatrix() を呼び出すために, この関数の宣言をメインプログラムに追加します.

...
 
/*
** 投影変換行列
*/
extern void orthogonalMatrix(float left, float right,
                             float bottom, float top,
                             float near, float far,
                             GLfloat *matrix);
extern void perspectiveMatrix(float left, float right,
                             float bottom, float top,
                             float near, float far,
                             GLfloat *matrix);
static GLfloat projectionMatrix[16];
static GLint projectionMatrixLocation;
 
...

そして, 平行投影変換行列 orthogonalMatrix() を呼び出している部分を, perspectiveMatrix() に置き換えます.

  ...
  
  /* シェーダプログラムのリンク */
  glLinkProgram(gl2Program);
  glGetProgramiv(gl2Program, GL_LINK_STATUS, &linked);
  printProgramInfoLog(gl2Program);
  if (linked == GL_FALSE) {
    fprintf(stderr, "Link error.\n");
    exit(1);
  }
  
  /* 視野変換行列を求める */
  lookAt(4.0f, 5.0f, 6.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f, temp0);
  
  /* 透視投影変換行列を求める */
  perspectiveMatrix(-1.0f, 1.0f, -1.0f, 1.0f, 7.0f, 11.0f, temp1);
  
  /* 視野変換行列と投影変換行列の積を projectionMatrix に入れる */
  multiplyMatrix(temp0, temp1, projectionMatrix);
  
  /* uniform 変数 projectionMatrix の場所を得る */
  projectionMatrixLocation = glGetUniformLocation(gl2Program, "projectionMatrix");
  
  ...

これで透視投影変換による描画が行われるはずです. 下のような図形が描かれれば OK です.

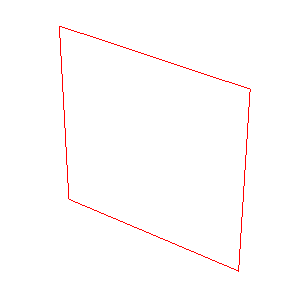
一応, ここまでのプログラムをまとめたものを, 以下に用意しておきます.

• Linux 版
• Mac OS X 版
• Windows 版