■ 2009年12月25日 [OpenGL][GLSL][ゼミ] 第15回 ポイントのアニメーション
あああまた年末だ
夏休みに何か始めて気がついたら年末になっているという状況には前にも陥った記憶があるのですが, 考えてみれば毎年こういうことを繰り返した挙句に除夜の鐘を聞いているわけで, このまま何の進歩もなく老いさらばえていくのかと半ばあきらめに似た感情を抱くとともに, 人生の悲哀を感じている今日この頃です.
ところで, 毎年同じことをしているといえば, 我が家では大晦日に焼肉とそばを食べ, 元旦にカレーを食べることが恒例となっているのですが, 知り合いには「それは正月の過ごし方として間違っている」と指摘されました. 別にいいじゃんと思っていたのですが, 先日通勤途中でこういうのぼりを見かけました.

正月にカレーを食べることは, 正式な日本の風習として認められています.
宇宙は美しい
ということで, 研究室の学生さん向け「夏休みゼミ」の続編の「冬休みゼミ」です. 私からのクリスマスプレゼントです. ありがたくないですかそうですかどうもすみません.
先日, 某所で国立天文台の Mitaka というソフトウェアを見せていただき, その美しさに魅了されて自分も点をいっぱい描いてみたくなりました. 大量の点でアニメーションするには, CPU による座標値の更新をできるだけ控えて, GPU (バーテックスシェーダ) で座標値の更新を行った方がよいようです. 確かに, この方が描画性能を上げやすい (少なくともビデオカードの性能を出しやすい) と予想されます.
CPU に頼らずバーテックスシェーダで座標値を逐次更新するには, 現在の座標値を GPU 側に保持しておく必要があります. これは Transform Feedback を使ってバーテックスシェーダでの計算結果をバッファオブジェクトに格納すれば実現できますが, ここでは座標を時間をパラーメータとする関数で表すことにします (腰砕けで悪いけど Transform Feedback もそのうち使ってみます). 以後, 以下の雛形をもとに解説します.
点で円柱を描く
とりあえず点をいっぱい描くプログラムを作ってみます. CPU から GPU への座標値 (頂点情報, attribute) の転送には, 夏休みゼミでやった頂点バッファオブジェクトを使います. バッファオブジェクトをプログラムのメモリ空間にマップし, そこに乱数で決定した座標値を格納します. 点を円柱状に散布 (撒布) するには, 一様乱数 u を用いて円柱座標系の座標値 (r, θ, h) を発生し, それを直交座標系 (x, y, z) に変換します.
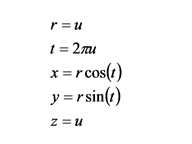
ただし, このままだと点の密度が中心からの距離 r に反比例して下がってしまうので, r として一様乱数 u の代わりに 2u の平方根を用います. これは r に比例した分布を持つ乱数になります.
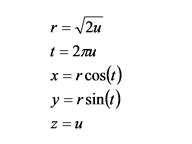
これにより, u が区間 [0, 1] に一様に分布する乱数であれば, 半径 1, 高さ 1 の円柱状の空間に点が散布されます.
確率密度関数 f(x) に従う分布を持つ乱数を発生するには, f(x) の累積分布関数,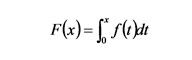
の逆関数 F-1(x) の引数に一様乱数 u を与えます. この方法は逆関数法と呼ばれます. f(x) = x なら,
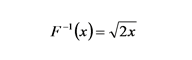
また球状に散布する場合は, f(x) = x2 なので,
となります.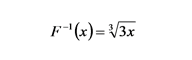
...
/* 頂点バッファオブジェクトのメモリを参照するポインタのデータ型 */
typedef GLfloat Point[3];
/*
** 点を空間に散布する
*/
GLuint disseminate(int points, const GLuint *buffer)
{
/* 頂点バッファオブジェクトを有効にする */
glBindBuffer(GL_ARRAY_BUFFER, buffer[0]);
/* 頂点バッファオブジェクトにメモリ領域を確保する */
glBufferData(GL_ARRAY_BUFFER, sizeof (Point) * points, NULL, GL_STATIC_DRAW);
/* 頂点バッファオブジェクトのメモリをプログラムのメモリ空間にマップする */
Point *point = (Point *)glMapBuffer(GL_ARRAY_BUFFER, GL_WRITE_ONLY);
/* 頂点の位置 */
for (int i = 0; i < points; ++i) {
float r = sqrt(2.0f * (float)rand() / ((float)RAND_MAX + 1.0f));
float t = 6.283185f * (float)rand() / ((float)RAND_MAX + 1.0f);
(*point)[0] = r * cos(t);
(*point)[1] = r * sin(t);
(*point)[2] = (float)rand() / ((float)RAND_MAX + 1.0f);
++point;
}
/* 頂点バッファオブジェクトのメモリをプログラムのメモリ空間から切り離す */
glUnmapBuffer(GL_ARRAY_BUFFER);
/* 頂点バッファオブジェクトを解放する */
glBindBuffer(GL_ARRAY_BUFFER, 0);
return points;
}
初期化時にこの関数 disseminate() を呼び出して頂点バッファオブジェクトに座標値を転送しておき, 描画時に glDrawArrays() によって点を描きます.
例によって, マウスの左ボタンでドラッグすれば, 図形を回転できます.
シェーダプログラム
点を打つだけですから, シェーダプログラムは非常に簡単です. バーテックスシェーダでは点の座標値を格納した attribute 変数 point を座標変換するだけです.
#version 120
//
// simple.vert
//
attribute vec3 point;
uniform mat4 transformMatrix;
void main(void)
{
gl_Position = transformMatrix * vec4(point, 1.0);
}
この個々の点の座標値を時間とともに変化させます. 現在時刻は uniform 変数 elapsedTime に得ることにします. これを point の z 座標値 point.z から引いて, 描画する点の位置を変化させます. point.z は [0, 1) の区間にありますから, 移動後の位置がこの範囲からはみ出ないように, GLSL の組み込み関数 fract() を使って小数点以下のみを取り出します.
#version 120
//
// simple.vert
//
attribute vec3 point;
uniform float elapsedTime;
uniform mat4 transformMatrix;
void main(void)
{
float z = fract(point.z - elapsedTime);
gl_Position = transformMatrix * vec4(point.xy, z, 1.0);
}
フラグメントシェーダではフラグメントに白色を設定するだけです.
#version 120
//
// simple.frag
//
void main(void)
{
gl_FragColor = vec4(1.0);
}
時間を計る
次に, プログラム実行中の経過時間を求め, シェーダプログラムの uniform 変数 elapsedTime に格納します. そのために, まず, uniform 変数 elapsedTime の場所を求め, 変数 elapsedTimeLocation に保存しておきます. elapsedTimeLocation は後で定義します.
...
/*
** 初期化
*/
static void init(void)
{
...
/* シェーダプログラムのリンク */
glLinkProgram(gl2Program);
glGetProgramiv(gl2Program, GL_LINK_STATUS, &linked);
printProgramInfoLog(gl2Program);
if (linked == GL_FALSE) {
fprintf(stderr, "Link error.\n");
exit(1);
}
/* uniform 変数 elapsedTime の場所を得る */
elapsedTimeLocation = glGetUniformLocation(gl2Program, "elapsedTime");
/* uniform 変数 transformMatrix の場所を得る */
transformMatrixLocation = glGetUniformLocation(gl2Program, "transformMatrix");
...
GLUT では glutGet(GLUT_ELAPSED_TIME) により経過時間をミリ秒単位で得ることができます. これを関数 init() の最後のほうで一度だけ呼び出しておきます.
... /* トラックボール処理の初期化 */ trackball.initialize(); /* 経過時間の初期化 */ glutGet(GLUT_ELAPSED_TIME); /* 背景色 */ glClearColor(0.0, 0.1, 0.3, 1.0); } ...
描画時に glutGet(GLUT_ELAPSED_TIME) を呼び出せば, 最初に glutGet(GLUT_ELAPSED_TIME) を呼び出してからの経過時間を得ることができます. 記号定数 CYCLE は変数 elapsedTime が 1 増えるのに要する時間で, アニメーションの速度調整に使います. これも後で定義します.
...
/*
** 画面表示
*/
static void display(void)
{
/* 投影変換/視野変換/モデリング変換 */
Matrix transformMatrix = projectionMatrix * modelviewMatrix * trackball.get();
transformMatrix.scale(1.0f, 1.0f, 2.0f);
transformMatrix.translate(0.0f, 0.0f, -0.5f);
/* シェーダプログラムを適用する */
glUseProgram(gl2Program);
/* 経過時間を求める */
float elapsedTime = (float)glutGet(GLUT_ELAPSED_TIME) / CYCLE;
/* uniform 変数 elapsedTime に時間を設定する */
glUniform1f(elapsedTimeLocation, elapsedTime);
/* uniform 変数 transformMatrix に行列を設定する */
glUniformMatrix4fv(transformMatrixLocation, 1, GL_FALSE, transformMatrix.get());
/* attribute 変数 point に頂点情報を対応付ける */
glEnableVertexAttribArray(pointLocation);
...
最後に変数 elapsedTimeLocation と記号定数 CYCLE を定義します. CYCLE は 5,000 ミリ秒にしておきます.
... /* ** 点の数 */ #define POINTS 100000 /* ** 経過時間 */ static GLint elapsedTimeLocation; #define CYCLE 5000.0f /* **トラックボール処理 */ #include "Trackball.h" static Trackball trackball; static int pressedButton; ...
こういうアニメーションになります. マウスでぐるぐる回してみてください. 上等なビデオカードを使っている人は, main.cpp の最初のほうで定義している記号定数 POINTS を 1000000 とか 10000000 とかにして速さを堪能してみてください.
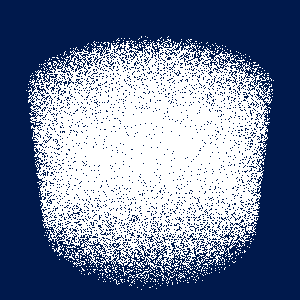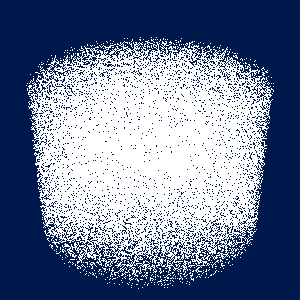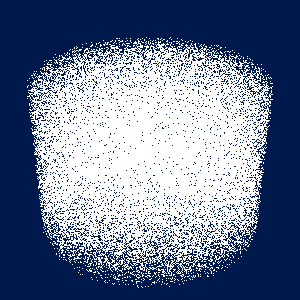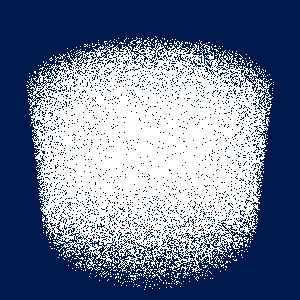
渦を描いてみる
それではバーテックスシェーダを変更して, 下図のような渦を描いてみてください. 点の x 座標値と y 座標値をそれぞれ z2 倍すれば, この図のように円柱の半径を「絞る」ことができます.
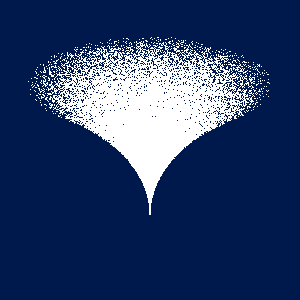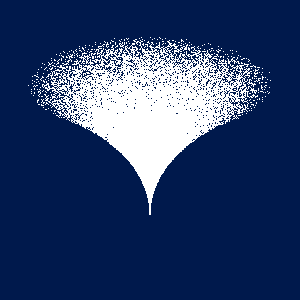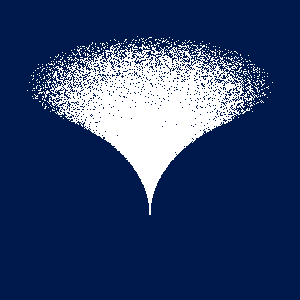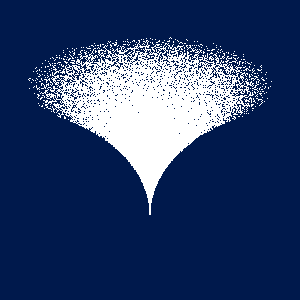
円(柱)内の一様乱数のコードですけど、これだと半径√2の円になってしまいますね。<br>乱数の定義域を0.5 * 半径の二乗に修正するのが正しいコードだと思われます。
猫式さま、ご指摘ありがとうございます。おっしゃる通り、このプログラムでは r=√2u を正規化していませんでした。
猫式さま、すみません、おっしゃりたいこと分かりました。逆関数法で値域と定義域が入れ替わってるのに、元の値域の [0, 1] をそのまま定義域に使うのはまずい、という話ですね。r=√2u で r の値域を [0, 1] にしたいなら、u の定義域を [0, 1/2] にせよと。おっしゃる通りです。素直に r=R√u とすべきでした。