床井研究室

ベイ・マックス

ベイ・マックス見たわけですよ. すごかったすよ. 2014 年の映画としては, 男子としては男が添え物と言われる「アナ雪」よりよっぽど面白かったし, 技術的にも CG に関わっている身としてはいろいろ悔しいなぁと思うところもありました. また, 自分の立場としてもオープニングの「大学」の描かれ方にグッとくるものがあって, もっと頑張らなきゃって無闇にテンション上げられてしまいました.

んで, そのオープニングで主人公のヒロがキャラハン教授と出会った時に発した「キャラハン-キャットムル曲線の！」というセリフで, もう自分の顔がゆるみまくってるのを矯正できずに困ってしまいました. あー, WALL-E の起動音といい, どうしてこういう限定された相手にしか通じない？ような細かいネタを仕込んでくるかなぁ. そう, "キャットムル" は CG の研究者であり PIXER の創業者であり, 現在はウォルト・ディズニー・アニメーション・スタジオの社長も務めてる Edwin Catmull 氏であって (って 1 年生にはこれから授業で話す予定), 氏の数多くの業績の一つに Catmull-Rom 曲線ってのがあります (これは 3 年生と M1 にはもう授業で話した).

だから, 思わずつぶやいちゃったよ…

髪の毛の細分割

さらに言うと, この Catmull-Rom 曲線をこの髪の毛のシリーズで使おうと思ってたところだったので, そのあとドキドキしちゃった. んでね, なんでこれを使おうかと思ったかというと, やっぱり物理シミュレーションは重いわけで, それにゲームなんかだと他にもやらなきゃいけない処理もいろいろあるわけで, やっぱり何とかして処理を軽くしたいって思うわけですよ. それには単純に力の計算の対象となる節点の数を減らすのが一番手っ取り早いんですけど, そうすると角が見えたり陰影が汚くなったりして, 見栄えが悪くなってしまいます. 実際, 前回追加した陰影は, あまり滑らかではありませんでした.

• 陰影の計算を追加したプログラム

そこで節点を通る曲線を求め, それを細分割することにより, 滑らかな髪の毛を表現してみようと思います. この辺の話は (この辺に限らず髪の毛には) もう国内*1外*2に山のように文献があって, SIGGRAPH 2008 の Cource Note*3 見ただけで目が回りそうです*4.

三次 Hermite 曲線

Catmull-rom 曲線の説明の前に, 三次 Hermite (エルミート) 曲線について説明します.

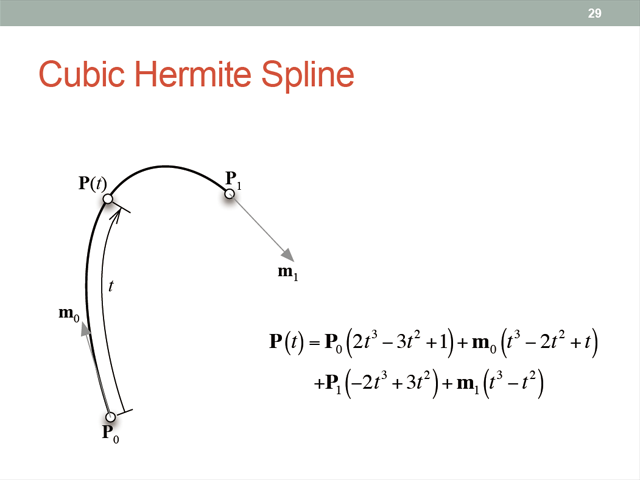
導き方はエルミート曲線軌道で詳しく解説されています. 2 点 P₀, P₁ を結び, P₀ における接線が m₀, P₁ における接線が m₁ となる曲線

P(t), t ∈ [0, 1]

を考えます. P(t) が t の 3 次関数なら,

P(t) = at3 + bt2 + ct + d

と書くことができます. したがって,

P0 = P(0) = d
P1 = P(1) = a + b + c + d

となります. 次に, P(t) を t で微分すると

P'(t) = 3at2 + 2bt + c

となりますから,

m0 = P'(0) = c
m1 = P'(1) = 3a + 2b + c

となります. これらから c と d を消去すると, 次の連立方程式が得られます.

P1 - P0 = a + b + m0
m1 - m0 = 3a + 2b

これを解けば,

a = 2(P0 - P1) + m0 + m1
b = -3(P0 - P1) - 2m0 - m1
c = m0
d = P0

となります. これを整理して, P(t) は前の図中の式のように表されます.

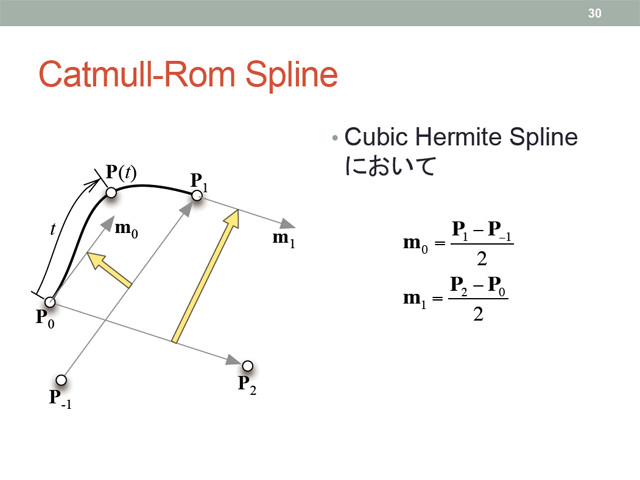
Catmull-Rom 曲線

Catmull-Rom 曲線は点 P_i における接線 m_i に, P_i のひとつ前の点 P_{i - 1} から一つ先の点 P_{i + 1} に向かうベクトルを, そのパラメータ t の定義域の大きさで割ったものを用います. t ∈ [0, 1] であれば, ひとつ前の点と結ぶ曲線 P_{i - 1}(t) = P_i(t - 1), 一つ次の点と結ぶ曲線 P_{i + 1}(t) = P_i(t + 1) と考えて, 定義域の大きさは 2 とします.

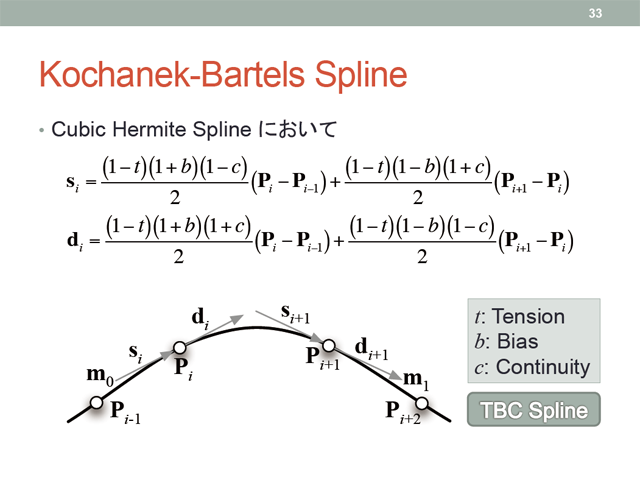
なお, m₀, m₁ のそれぞれに重み (1 - w) をかけたものを Cardinal Spline といい, w = 1 で折れ線, w = 0 で Catmull-Rom 曲線と同じになります. この w はこの点における張り (Tension) になります. さらに偏り (Bias) や連続性 (Continuity) も制御できるようにしたものは Kochanek-Bartels Spline と呼びます. これは TBC スプラインとして知られています.

ジオメトリシェーダの追加

節点を Catmull-Rom 曲線で補間して線分を細分化する処理は, ジオメトリシェーダで行います. それに伴い, これまでバーテックスシェーダで行っていた処理は細分化により生成した線分に対して行うため, ジオメトリシェーダに移します. バーテックスシェーダでは与えられた頂点属性 (節点の位置) をそのままジオメトリシェーダに送ります.

#version 150 core
#extension GL_ARB_explicit_attrib_location : enable
 
// 頂点属性
layout (location = 0) in vec4 position;             // 節点のローカル座標系での位置
 
void main()
{
  // 視点座標系の座標値
  gl_Position = position;
}

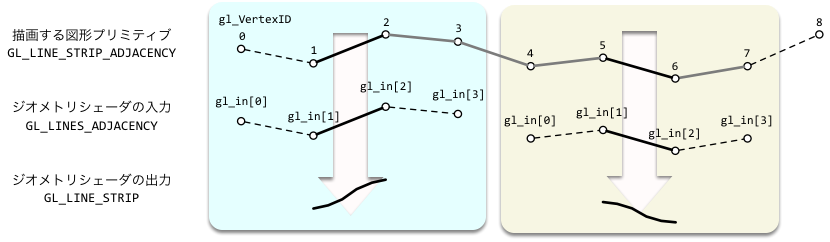
ジオメトリシェーダのソースファイル hair.geom を新たに追加します. Catmull-Rom 曲線では, 曲線の両端点のほかに, 始点のひとつ前の点と終点の一つ先の点が必要になります. したがって, ジオメトリシェーダへの入力となる図形プリミティブに GL_LINES_ADJACENCY を使う必要があります. 詳しくは 2009 年 8 月 28 日の記事を参照してください. "layout (lines_adjacency) in;" はジオメトリシェーダに入力する図形プリミティブに GL_LINES_ADJACENCY を使用します. また, "layout (line_strip, max_vertices = 20) out;" によりジオメトリシェーダから出力する図形プリミティブとして GL_LINE_STRIP を指定します. max_vertices = 20 はこのジオメトリシェーダ内で生成される頂点属性の最大数です.

#version 150 core
#extension GL_ARB_explicit_attrib_location : enable
 
layout (lines_adjacency) in;
layout (line_strip, max_vertices = 20) out;

定数として, 新たに曲線の分割数 division を定義しておきます. また, ジオメトリシェーダでは隣接する頂点の情報をジオメトリシェーダ内で取得できますから, テクスチャバッファオブジェクトを参照する必要がありません. したがって, そのために使っていた uniform 変数の neighbor と endpoint は削除します. その他の定数, uniform 変数, out 変数は, バーテックスシェーダのものをそのまま移します.

// 定数
const int division = 4;                             // 曲線の分割数
const vec4 pl = vec4(1.0, 6.0, 4.0, 1.0);           // 光源位置
 
// uniform 変数
uniform mat4 mc;                                    // ビュープロジェクション変換行列
 
// ラスタライザに送る頂点属性
out vec3 v;                                         // 視線ベクトル
out vec3 l;                                         // 光線ベクトル
out vec3 t;                                         // 接線ベクトル

あらかじめ m0 = (P₁ - P_-1) / 2, m1 = (P₂ - P₀) / 2, および dp = P₀ - P₁ を求め, それらから a, b, c, d を求めておきます.

void main()
{
  vec4 m0 = (gl_in[2].gl_Position - gl_in[0].gl_Position) * 0.5;    // (P1 - P-1) / 2
  vec4 m1 = (gl_in[3].gl_Position - gl_in[1].gl_Position) * 0.5;    // (P2 - P0) / 2
  vec4 dp = gl_in[1].gl_Position - gl_in[2].gl_Position;            // P0 - P1
  vec4 a = 2.0 * dp + m0 + m1;
  vec4 b = -3.0 * dp - 2.0 * m0 - m1;
  vec4 c = m0;
  vec4 d = gl_in[1].gl_Position;

曲線の分割数 division + 1 (生成する頂点の数) だけ繰り返します. i = 0 と i = division の場合をループの外に出して補間計算を省くことができますが, めんどくさいのでループの中に入れたままにしています. ループの中では節点の位置 position とその点における接線ベクトル t を, それぞれ Catmull-Rom 曲線の式およびそれを t で微分した式で求めます. その他はバーテックスシェーダでの処理をそのまま移します. ループの最後で EmitVertex() を呼び出して頂点を生成した後, バーテックスシェーダの最後で EndPrimitive() を呼び出します*5.

  for (int i = 0; i <= division; ++i)
  {
    float s = float(i) / float(division);
    
    // Catmull-Rom 曲線
    vec4 position = ((a * s + b) * s + c) * s + d;
    
    // スクリーン座標系の座標値
    gl_Position = mc * position;
    
    // 視線ベクトルは頂点位置の逆ベクトル
    v = -normalize(position.xyz);
    
    // 光線ベクトルは頂点から光源に向かうベクトル
    l = normalize((pl - position * pl.w).xyz);
    
    // 接線ベクトルは Catmull-Rom 曲線 の微分
    t = normalize(((3.0 * a * s + 2.0 * b) * s + c).xyz);
    
    // 頂点の出力
    EmitVertex();
  }
  
  // 図形の終了
  EndPrimitive();
}

メインプログラムの修正

ジオメトリシェーダの追加に伴って, main.cppp も修正します. まず, プログラムオブジェクトの作成時に hair.vert も指定します. uniform 変数 neighbor と endpoint は削除しましたから, その場所の取り出しも削除します.

  ...
  
  //
  // プログラムオブジェクト
  //
  
  // 描画用のシェーダプログラムを読み込む
  const GLuint hairShader(ggLoadShader("hair.vert", "hair.frag", "hair.geom"));
  const GLint hairMcLoc(glGetUniformLocation(hairShader, "mc"));
  
  // 節点に加わる力の計算用のシェーダプログラムを読み込む
  
  ...

通常の描画時にテクスチャバッファオブジェクトを参照しないようになりましたから, uniform 変数の設定やテクスチャバッファオブジェクトの結合などの処理は削除します. また, 図形ごとの uniform 変数の設定が不要になったので, 描画に glMultiDrawArrays() が使えます. あと, ジオメトリシェーダの入力図形として GL_LINES_ADJACENCY を指定したので, ここでは GL_LINE_STRIP_ADJACENCY を使って描画します.

    ...
    
    //
    // 通常の描画
    //
    
    // 頂点配列オブジェクトを選択する
    glBindVertexArray(vao[buffer]);
    
    // 描画用のシェーダプログラムを使用する
    glUseProgram(hairShader);
    
    // ビュープロジェクション変換行列を設定する
    glUniformMatrix4fv(hairMcLoc, 1, GL_FALSE, mc.get());
    
    // 頂点配列を描画する
    glMultiDrawArrays(GL_LINE_STRIP_ADJACENCY, first.data(), count.data(), hairNumber);
    
    // フレームバッファを入れ替える
    window.swapBuffers();
    
    ...

• 髪の毛を曲線で補間したプログラム

禿げている

いや本当に最近の自撮り写真で禿げが目立ってきて落ち込んでいます. 正月に帰省して, 母親にまで「禿げたねぇ」としみじみ言われ, 追い打ちをかけられました… という話ではなくて, GL_LINE_STRIP_ADJACENCY を使って描画するようにしたので, 折れ線の根元の線分と先端の線分が描かれません. 先っぽは, まあ諦めてもらうとして (どうしてだ), 最初の線分が描かれないことによって, つむじの部分の禿げが広がっています. これは曲げ方向の力を考慮する際になんとかしようと思っています.

現場に行きたい

ベイ・マックスを見て, やっぱり自分は CG の制作に関わりたいんだと改めて思いました. また Rhizomatiks の仕事を見て, 自分も自分なりの表現をプログラムとして実装したいんだと焦り始めています. でも, もう年齢が年齢だけに, 自分の現状を変更する勇気ってのはありません. だから, 少しでも現場を見て, 人に会って, 見てきたことを学生さんに伝えたいと思っています.