床井研究室

やりたいことがいっぱいある

本当にやりたいことはいっぱいあって，いくつかには手を付けたものの，やらなきゃなんないことに時間を奪われて，途中で放置している状態です．でも，一番やりたかった「家族と一緒に版ご飯を食べる」は，このところ実践しています．やりたいことをやる時間がなければ，やらなきゃなんないことに混ぜてやってしまえとか思うんですけど，なかなかうまくいきませんね．学生さん向けの資料もいくつかブログにまとめようと思っているんですけど，後回しになっています．GLFW で Oculus を使うことに関しても，それなりにノウハウがたまってきたのでブログにまとめたいと思ってるんですけど．

魚眼レンズ

その関連で，最近はやりの RICOH THETA S や Kodak SP360 4K で撮った全方位画像 (っていうのが画像処理的な言い方なのかなと思いますけど，一般的には全天球画像とか全周画像とか言いますね) を Oculus Rift DK1 / DK2 で見る方法について，「私のやり方」をちょっとでメモっておこうと思います．魚眼レンズ画像というのは，例えばこんなものです．これは11年前! (自分でもちょっとびっくり) に放物面マッピングの記事を書いたときに使ったものです．画像の上下が反転しているのは OpenGL の都合です．

これは魚眼レンズを付けた Nikon COOLPIX 995 で撮影しました．

このカメラとレンズは私の持ち物ではないのですが，同僚から借りたまま，今でも放射照度マッピングの素材作成などに使っています*1．でも最近，RICOH THETA S と Kodak SP360 4K を買ったので，いい加減，持ち主に返そうかと思っています．11 年ぶりに．

この Nikon COOLPIX 995 の魚眼レンズを含め，現在一般に市販されている魚眼レンズの大半は，画像の中心からの距離が角度に比例する等距離射影方式のものです．他の射影方式のものは，カメラ用では等立体角射影方式の SIGMA 4.5mm F2.8 EX DC CIRCULAR FISHEYE HSM くらいしか知りません．ググると FIT FI-085／111 というものが見つかります．これは射影方式を切り替えられるようなので，このあたりの沼にはまるには最適かと思います．誰か買ってください．なお，レンズの射影方式については，屋根の上さんが詳しいです．

魚眼レンズ画像の平面展開

この画像を平面に展開して投影するわけですが，ディスプレイが Oculus Rift などの HMD の場合，ヘッドトラッキングによって取得した頭の方向を使って，見ている方向の映像を表示する必要があります．

そこで，ディプレイの視野 (Fov, Field of View) を，次のような四角錐でモデル化します．この四角錐の頂上は原点にあり，視点はそこにあります．

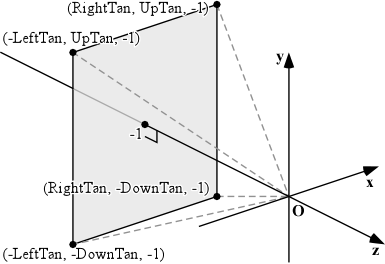
一方，ディスプレイの全面を埋めるポリゴンを描くには，クリッピング空間の xy 平面に一致する四角形を用います．

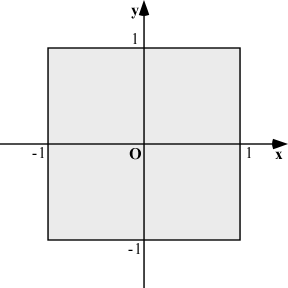
バーテックスシェーダ

バーテックスシェーダでは，この頂点座標を pv という attribute 変数で受け取るとします．これをそのまま gl_Position に代入すれば，クリッピング空間いっぱい，すなわち表示領域の全面を埋めるポリゴンを描くことができます．そのとき，同時にこの四角形の頂点位置から，視野の四角錐の底面の頂点座標を求めます．

$$\begin{array}{l}texcoord_x=\frac{RightTan+LeftTan}{2}pv_x+\frac{RightTan-LeftTan}{2}\\texcoord_y=\frac{UpTan+DownTan}{2}pv_y+\frac{UpTan-DownTan}{2}\\texcoord_z=-1\end{array}$$

これを Oculus のヘッドトラッキングにより得た回転行列 mo*2 を使って回転し，それを varying 変数 texcoord に out します．その際，全方位画像の場合は画像は無限の遠方にあると考えますので，ヘッドトラッキングの平行移動成分は使用しません*3．

#version 150 core
#extension GL_ARB_explicit_attrib_location : enable
 
//
// tracking.vert
//
//   ヘッドトラッキングを行う
//
 
// 頂点座標
layout (location = 0) in vec4 pv;
 
// Oculus Rift の回転
uniform mat4 mo;
 
// スクリーンのサイズと中心位置
uniform vec4 screen;
 
// テクスチャ座標
out vec3 texcoord;
 
void main()
{
  // 頂点座標を方向ベクトルに換算
  texcoord = vec3(mo * vec4(pv.xy * screen.xy + screen.zw, -1.0, 0.0));
  
  // 頂点座標をそのまま出力
  gl_Position = pv;
}

ここで screen には vec4((RightTan + LeftTan) * 0.5, (UpTan + DownTan) * 0.5, (RightTan - LeftTan) * 0.5, (UpTan - DownTan) * 0.5) を格納しています．

フラグメントシェーダ

こうするとフラグメントシェーダで受け取った varying 変数 texcoord の内容は，そのフラグメントを通る視線の方向ベクトルになります．これを使ってテクスチャをサンプリングします．

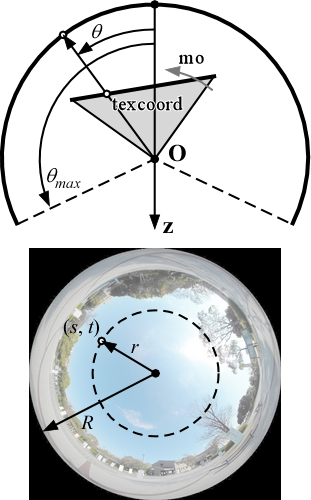
魚眼レンズ画像のイメージサークルの半径を R，そこにおける仰角を θ_max とすれば，texcoord の方向 (視線の方向) のテクスチャ座標値 (s, t) は次式で求めることができます．

$$\begin{array}{l}\theta=\arccos\left\{\frac{-texcoord_x}{\sqrt{texcoord_x^2+texcoord_y^2+texcoord_z^2}}\right\}\\r=\frac{\theta}{\theta_{max}}R\\s=\frac{texcoord_x}{\sqrt{texcoord_x^2+texcoord_y^2}}r\\t=\frac{texcoord_y}{\sqrt{texcoord_x^2+texcoord_y^2}}r\end{array}$$

#version 150 core
#extension GL_ARB_explicit_attrib_location : enable
#extension GL_ARB_explicit_uniform_location : enable
 
//
// fisheye.frag
//
//   魚眼レンズを使って撮影した画像を用いる
//
 
// テクスチャ
layout (location = 3) uniform sampler2D image;
 
// 背景テクスチャのシフト量
uniform vec2 shift;
 
// 背景テクスチャのスケールと中心位置
uniform vec2 scale;
 
// ラスタライザから受け取る頂点属性の補間値
in vec3 texcoord;                                   // テクスチャ座標
 
// フレームバッファに出力するデータ
layout (location = 0) out vec4 fc;                  // フラグメントの色
 
// 天頂角 (θmax) の逆数
const float invTmax = 0.6366198;
 
void main(void)
{
  // このフラグメントを通る視線の方向ベクトル
  vec3 direction = normalize(texcoord);
  
  // テクスチャ座標
  vec2 st = normalize(texcoord.xy) * acos(-direction.z) * invTmax;
  
  // 全周魚眼画像から視線方向の色をサンプリングする
  fc = texture(image, st * scale + shift);
}

これは θ_max = 90° (180° 全周魚眼レンズ) の場合です．invTmax = 1 / (π / 2) = 0.6366198 です．

Kodak SP360 4K の場合は，レンズカバーを付けていない場合（下図はレンズカバー付き），θ_max は手振れ補正 off のとき 235° / 2 = 117.5°，on のとき 206° / 2 = 103° なので，invTmax はそれぞれ 0.4876237，0.5562697 くらいになります．

scale はイメージサークルの拡大率を微調整するパラメータで，初期値は (0.5, 0.5) です．shift はイメージサークルの中心位置を微調整するパラメータで，これも初期値は (0.5, 0.5) です．

RICOH THETA S のライブストリーミングの場合

RICOH THETA S は，静止画では正距円筒図法の画像が得られますが，ライブストリームでは二つの全周魚眼 (Dual Fisheye) 画像が得られます．この個々のイメージサークルは θ_max = 90° (180° 全周魚眼レンズ) として扱い，その角度における画像の半径を R とします．実際のイメージサークルは R の範囲より広くなっています．

フラグメントシェーダでは，処理対象のフラグメントにおける視線の方向ベクトルから，全天球の「北極」と「南極」からの角度 θ と θ' を求めます．そして，そのそれぞれについてイメージサークルの中心からの距離 r と r'，テクスチャ座標 (s, t) と (s', t') を求め，テクスチャの二か所をサンプリングします．この一方が R の内部にあれば，もう一方は R の外部にあります．r，r' が R に近い場合は両方の画像がサンプリングされるので，R の付近でスロープになっている階段状の関数を使って，これらをブレンドします．

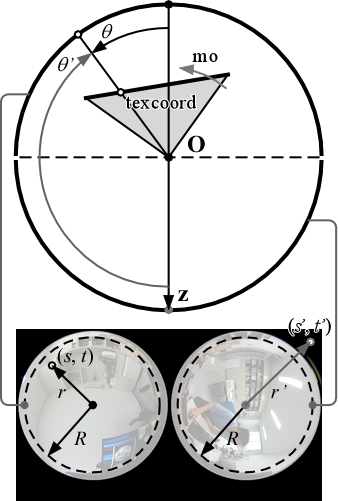
フラグメントシェーダのプログラムは，次のようになります．

#version 150 core
#extension GL_ARB_explicit_attrib_location : enable
#extension GL_ARB_explicit_uniform_location : enable
 
//
// thetalive.frag
//
//   RICOH THETA S のライブストリーミング映像を用いる
//
 
// テクスチャ
layout (location = 3) uniform sampler2D image;
 
// 背景テクスチャのシフト量
uniform vec2 shift;
 
// 背景テクスチャのスケールと中心位置
uniform vec2 scale;
 
// ラスタライザから受け取る頂点属性の補間値
in vec3 texcoord;                                   // テクスチャ座標
 
// フレームバッファに出力するデータ
layout (location = 0) out vec4 fc;                  // フラグメントの色
 
void main(void)
{
  // このフラグメントを通る視線の方向ベクトル
  vec3 direction = normalize(texcoord);
  
  // この方向ベクトルの相対的な仰角 [-1, 1]
  float angle = acos(direction.z) * 0.63661977 - 1.0;
  
  // 前後のテクスチャの混合比
  float blend = 0.5 - clamp(angle * 10.0, -0.5, 0.5);
  
  // 視線の方向ベクトルの yx 平面上での方位ベクトル
  vec2 orientation = normalize(texcoord.yx) * 0.885;
  
  // 二重魚眼テクスチャのサイズ
  vec2 size = vec2(textureSize(image, 0));
  
  // 魚眼画像のイメージサークルの高さの２分の１
  float aspect = size.x * 0.25 / size.y;
  
  // 前後のイメージサークルの半径
  vec2 radius_f = vec2( 0.25, aspect);
  vec2 radius_b = vec2(-0.25, aspect);
  
  // 前後のイメージサークルの中心
  vec2 center_f = vec2(0.75, aspect);
  vec2 center_b = vec2(0.25, aspect);
  
  // 前後のテクスチャの色をサンプリングする
  vec4 color_f = texture(image, (1.0 - angle) * orientation * radius_f + center_f);
  vec4 color_b = texture(image, (1.0 + angle) * orientation * radius_b + center_b);
  
  // サンプリングした色をブレンドしてフラグメントの色を求める
  fc = mix(color_f, color_b, blend);
}

こんな具合にできます．このやり方で 2 台の THETA S から HDMI でライブストリーミングした映像をリアルタイムに展開しても，特に重いということはありませんでした．

実は THETA S ２個使えたり． pic.twitter.com/i4KdCKYgAv

— 床井浩平 (@tokoik) 2016年6月29日

本題とは関係ありませんが，このプログラムは Oculus Rift を２台使えます．PC も２台使いますけど…

Oculus Rift も２個使えたり (PC ２台だけど) pic.twitter.com/HmjcdA5V8V

— 床井浩平 (@tokoik) 2016年6月29日

正距円筒図法の場合

このように魚眼カメラで取得した画像は，正距円筒図法に変換しなくても，そのまま使うことができます．正距円筒図法の画像を使う場合は，フラグメントシェーダは以下のようになります．

#version 150 core
#extension GL_ARB_explicit_attrib_location : enable
#extension GL_ARB_explicit_uniform_location : enable
 
//
// theta.frag
//
//   RICOH THETA S を使って撮影した画像を用いる
//
 
// テクスチャ
layout (location = 3) uniform sampler2D image;
 
// 背景テクスチャのシフト量
uniform vec2 shift;
 
// 背景テクスチャのスケールと中心位置
uniform vec2 scale;
 
// ラスタライザから受け取る頂点属性の補間値
in vec3 texcoord;                                   // テクスチャ座標
 
// フレームバッファに出力するデータ
layout (location = 0) out vec4 fc;                  // フラグメントの色
 
void main(void)
{
  // 正距円筒図法画像から視線方向の色をサンプリングする
  fc = texture(image, atan(texcoord.xy, vec2(texcoord.z, length(texcoord.xz))) * vec2(-0.15915494, -0.31830989) + 0.5);
}

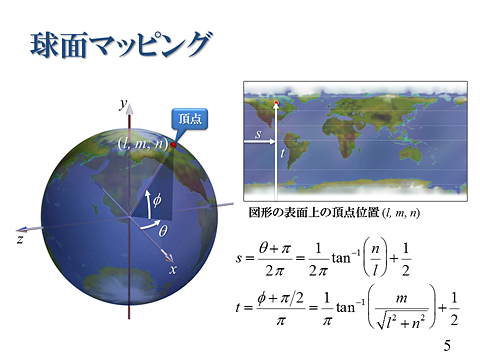
やってることは授業でやってることと同じです．「頂点」が球面上ではなく平面上（投影面上）にあるだけです．プログラム中の -0.15915494 = -1 / 2π，-0.31830989 = -1 / π です．

バーテックスシェーダで実装する

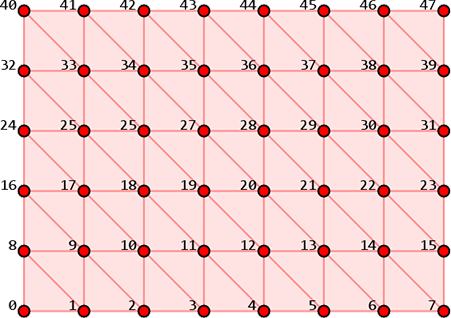
ここでは１枚ポリゴンを使用し，フラグメントシェーダでテクスチャ座標を算出しました．しかし，この１枚ポリゴンをメッシュに分割して描画し，バーテックスシェーダでテクスチャ座標 (s, t) まで求めておくこともできます．これを varying 変数として out すればラスタライザがテクスチャ座標を補間してくれるので，フラグメントシェーダの処理はテクスチャのサンプリングだけになり，処理を軽くすることができます．