床井研究室

車輪の再発明

研究をしていて一番めげるのは，自分の研究テーマに対して他の人がすでに成果を出していたことに気づいたときでしょうか．まあ，そうならないようにちゃんとサーベイをして，ということになるんでしょうけど，私のような凡人が思いつくことは他の誰もが思いつくことばかりなので，サーベイをすればするほど，また落ち込むことになります．

大体，関心の高い領域には多くの研究者が集まっているので，その分多くの成果が出ていて現状を追っかけるだけで精一杯になったりします．それで誰も関心を持ってないようなニッチな領域にテーマを見つけて，チマチマとした研究をやったりするわけなんですけど，それはやっぱり誰の関心も引かないので，結局浮かばれません．それでも地道にやるしかないんですけど．

Schlick の近似

Phong の陰影付けモデルでは，鏡面反射強度の算出にべき乗を用いる必要があります．しかし，C や C++ に用意されているべき乗を求める関数 pow() は，例えば一旦対数をとってから掛け算し，その指数をとるといった，結構回りくどい実装になっていたりします．だから，計算を速くしたいときには，pow() ってのはできるだけ使いたくない関数なんです．

そこで今回は，この pow() の代わりに Schlick の近似と呼ばれる関数を使ってみたいと思います．Schlick の近似をユーザ定義関数として定義して，前回の似非異方性反射の計算に応用します．

ユーザ定義関数

GLSL のユーザ定義関数は，基本的には C や C++ のものと変わりませんが，GLSL はポインタ型を持たないため，引数の参照渡しができません．そのため，引数を介して値を関数の呼び出し側に戻す場合や，それと値渡しとを区別するために，引数に in，out，あるいは inout という修飾子を付けます．

in

引数を値渡しで用います．仮引数への代入は，実引数には反映されません．仮引数の値を変更しない場合は，さらに const を指定することができます．

out

仮引数への代入は，メインプログラムに戻る際に実引数に反映されます．実引数は変数である必要があります．関数の呼び出し時には，この仮引数の値は未定義です．

inout

仮引数への代入は，メインプログラムに戻る際に実引数に反映されます．実引数は変数である必要があります．関数の呼び出し時には，この仮引数には実引数の値が格納されています．

フラグメントシェーダの変更

関数 shlick() を定義して，pow() を置き換えます．

// bump.frag
 
uniform sampler2D texture;
 
varying vec3 light;
varying vec3 view;
 
float shlick(const in float t, const in float k)
{
  return t / (k - k * t + t);
}
 
void main (void)
{
  vec4 color = texture2DProj(texture, gl_TexCoord[0]);
  vec3 fnormal = vec3(color) * 2.0 - 1.0;
  vec3 flight = normalize(light);
  float diffuse = dot(flight, fnormal);
  
  gl_FragColor = gl_FrontLightProduct[0].ambient;
  if (diffuse > 0.0) {
    vec3 fview = normalize(view);
    vec3 halfway = normalize(flight - fview);
    float specular = shlick(max(dot(fnormal, halfway), 0.0), 
                            halfway.y * halfway.y * gl_FrontMaterial.shininess);
    gl_FragColor += gl_FrontLightProduct[0].diffuse * diffuse
                 + gl_FrontLightProduct[0].specular * specular;
  }
}

一応，これでも前回と同じようなハイライトが出ます．比較すると，明るい部分が少し広がっているようです．時間を計ったわけではないので，速くなったかどうかはわかりません．GPU の pow() はかなり高速にできているようですし．

• Linux 版
• Windows 版

回転楕円面による近似

実は私も，以前 pow() の代わりに使える関数はないかなぁと考えたことがあります．それで，鏡面反射成分のローブを回転楕円面に見立てて，こういう式を導いてこっそり？使ってました．

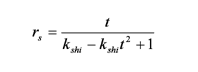
見てのとおり，Schlick の近似に似てます．でも，Schlick の近似の方が掛け算が１個少なくてすみます．それと，Schlick の近似が K_shi = 0 の時に Phong のモデルと同様に r_s = 1 になるのに対して，この式は回転楕円面から出発しているので r_s = t (= cosφ) になってしまうあたりが違います．Schlick の近似がどうやって導き出されたのか知りたかったんですが，Graphic Gems IV の Schlick の論文にはいきなり最後の式が出てました．

ところで，上記の式の導出は別に研究でもなんでもなかったんですが，それでも Shlick の近似の式を見たときは，「また（車輪の再発明を）やっちゃった」と恥ずかしくなった覚えがあります．冒頭の話は，ここから来ています．

いずれの式も k_shi を大きくすれば正規分布のようなベル形になるので，Phong のコサインモデルよりは現実の物体表面の性質を反映したものに近いんじゃないかなと思ってるんですけど，さあ，どうなんでしょう？誰か教えてください，偉い人．