床井研究室

日本橋

古いノートパソコンの増設メモリが和歌山で手に入らなかったので，先日，奥さんと一緒に大阪の日本橋にある中古パソコンショップに行きました．

その後，日本橋から難波に向かう途中に，メイド喫茶を見つけました．奥さんは「メイド喫茶がある！」と異様に反応していました．それをちょうど出勤してきた店員さんと思しきお姉さんに見とがめられ，「どうぞ〜，いらっしゃいませ〜」と声をかけられてしまいました．田舎者のオジサンはひきつりながら会釈を返しつつ，テンションが上がったオバサンを引きずって，その場を退散したのでした．しかし，お姉さんすっごくきれいだった．タレントさんみたい．

次に，奥さんのたっての希望で，四つ橋線で肥後橋へ．そして 30 分ほど行列に並んだ後，ついに，

Mon chou chou の堂島ロールゲット！，Get!，げっとぉぉぉ！！！！

和歌山のデパートでも数量限定で販売していたことが何回かあったのですが，いつも売り切れで涙を飲んでいたのでした（奥さんが）．さすがに人気だけのことはあります．クリームが一味違います．ミルク風味で，黒沢牧場のソフトクリームを連想しました．

GLSL による環境マッピング

学生さんに「何か説明して欲しいことは無いか？」と聞いたら「無い」というつれない返事だったので，何か適当なことを書くことにします．前に反射マッピング（リフレクションマッピング）については書きましたけど，屈折マッピング（リフラクションマッピング）については書いてませんでしたので，ちょっとまとめておきたいと思います．そのために，まず，以前作ったキューブマッピングによる環境マッピングのプログラムを，GLSL を使うように書き換えました．

• Linux 版
• Mac OS X 版
• Windows 版

単に書き換えるだけでなく，いろいろ細工しています（マウスの左ボタンでオブジェクト，右ボタンで背景を回転できるようになっています）．

このバーテックスシェーダプログラム reflect.vert は次のようになっています．

// reflect.vert
 
varying vec3 r;  // 視線の反射ベクトル
 
void main(void)
{
  vec4 p = gl_ModelViewMatrix * gl_Vertex;  // 頂点位置
  vec3 v = p.xyz / p.w;                     // 視線ベクトル
  vec3 n = gl_NormalMatrix * gl_Normal;     // 法線ベクトル
  r = vec3(gl_TextureMatrix[0] * vec4(reflect(v, n), 1.0));
  gl_Position = ftransform();
}

まず，頂点位置 gl_Vertex にモデルビュー変換行列を乗じて，視点座標系における頂点位置 p を求めます．視点座標系では視点は原点にありますから，視線ベクトル v は，この点の位置ベクトルになります．また，視点座標系における法線ベクトル n も求めておきます．n は正規化する必要がありますが，このプログラムでは形状データ作成の時点で頂点の法線ベクトルを正規化しているので，ここでは正規化していません．

そして，GLSL の組み込み関数 reflect() を使って，視線の反射ベクトルを求めます．これを使ってキューブマップをサンプリングすれば反射マッピングを実現できますが，ここではテクスチャを回転させるために，さらにテクスチャマトリクスを乗じています．この結果を varying 変数 r に格納して，フラグメントシェーダに渡します．

フラグメントシェーダプログラム reflect.frag では，この r を使ってキューブマップをサンプリングします．

// reflect.frag
 
uniform samplerCube cubemap;
 
varying vec3 r;  // 視線の反射ベクトル
 
void main(void)
{
  gl_FragColor = textureCube(cubemap, r);
}

屈折マッピング

GLSL の組み込み関数には，反射方向を求める reflect() の他に，屈折方向を求める refract() というものがあります．これを使って屈折マッピングを実現してみます．reflect.vert を次のように書き換えてください．

// reflect.vert
 
varying vec3 r;  // 視線の反射ベクトル
varying vec3 s;  // 視線の屈折ベクトル
 
const float eta = 0.67;  // 屈折率の比
 
void main(void)
{
  vec4 p = gl_ModelViewMatrix * gl_Vertex;
  vec3 v = normalize(p.xyz / p.w);
  vec3 n = gl_NormalMatrix * gl_Normal;
  r = vec3(gl_TextureMatrix[0] * vec4(reflect(v, n), 1.0));
  s = vec3(gl_TextureMatrix[0] * vec4(refract(v, n, eta), 1.0));
  gl_Position = ftransform();
}

視線の屈折ベクトルは，視線ベクトル v と法線ベクトル n を refract() の引数に与えて得ることができますが，refract() は refrect() と異なり，v を正規化しておく必要があります．eta は視線が通過する境界の前後にある媒質の屈折率の比で，視線が大気中からガラスに進入する場合，大気の屈折率 n₁ ≒ 1.0，ガラスの屈折率 n₂ ≒ 1.5 として，n₁ / n₂ ≒ 0.67 を設定しています．これらから得られた視線の反射ベクトルにテクスチャマトリクスを乗じて，結果を varying 変数 s に格納します．

フラグメントシェーダプログラム reflect.frag では，この s を使ってキューブマップをサンプリングします．

// reflect.frag
 
uniform samplerCube cubemap;
 
varying vec3 r;  // 視線の反射ベクトル
varying vec3 s;  // 視線の屈折ベクトル
 
void main(void)
{
  gl_FragColor = textureCube(cubemap, s);
}

この変更で，次のようが画像が得られます．

反射と屈折の合成

物体の境界面では，視線は反射方向と屈折方向に分かれるので，その点の色は反射方向にあるものの色と屈折方向にあるものの色を合成したものになります．そこで，試しにこれらを合成してフラグメントの色を決定するようにしてみましょう．フラグメントシェーダプログラムにおいて GLSL の組み込み関数 mix() を使って，反射方向にあるテクスチャのサンプル値と屈折方向にあるテクスチャのサンプル値を合成します．

// reflect.frag
 
uniform samplerCube cubemap;
 
varying vec3 r;  // 視線の反射ベクトル
varying vec3 s;  // 視線の屈折ベクトル
 
void main(void)
{
  gl_FragColor = mix(textureCube(cubemap, s), textureCube(cubemap, r), 0.5);
}

フレネル反射

前の例では，反射方向にあるテクスチャのサンプル値と屈折方向にあるテクスチャのサンプル値の配分を 0.5 に固定していましたが，この配分は，実際には視線の入射角と屈折率の比 (eta) で決まります．この関係はフレネルの式で求めることができます．以前，シェーダを使わずにこれを実装するために，この式の値を１次元テクスチャに格納しておく手法を用いましたが，シェーダが使えればこれをシェーダで計算することができます．ただし，フレネルの式は少し複雑なので，シェーダでは Shlick による近似（この人は Phong の陰影付けモデルを始め，いろんな式の近似式を提案している人ですね）が用いられるようです．

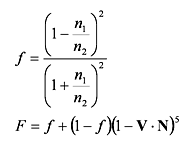
ここで f は視線が境界面に垂直に入射するときの反射率で，これはフレネルの式において入射角θ= 0 (c = v·h = 1) として求めることができます．V は視線ベクトルですが，ここでは参照点から視点に向かう単位ベクトルです．N は参照点における単位法線ベクトルです．これらをもとに参照点における反射率を求め，varying 変数 t に格納します．これをバーテックスシェーダプログラムに組み込むと，次のようになります．

// reflect.vert
 
varying vec3 r;  // 視線の反射ベクトル
varying vec3 s;  // 視線の屈折ベクトル
varying float t; // 境界面での反射率
 
const float eta = 0.67;  // 屈折率の比
const float f = (1.0 - eta) * (1.0 - eta) / ((1.0 + eta) * (1.0 + eta));
 
void main(void)
{
  vec4 p = gl_ModelViewMatrix * gl_Vertex;  // 頂点位置
  vec3 v = normalize(p.xyz / p.w);          // 視線ベクトル
  vec3 n = gl_NormalMatrix * gl_Normal;     // 法線ベクトル
  r = vec3(gl_TextureMatrix[0] * vec4(reflect(v, n), 1.0));
  s = vec3(gl_TextureMatrix[0] * vec4(refract(v, n, eta), 1.0));
  t = f + (1.0 - f) * pow(1.0 - dot(-v, n), 5.0);
  gl_Position = ftransform();
}

フラグメントシェーダプログラムでは，反射方向にあるテクスチャのサンプル値と屈折方向にあるテクスチャのサンプル値の合成に varying 変数 t を使うようにします．

// reflect.frag
 
uniform samplerCube cubemap;
 
varying vec3 r;  // 視線の反射ベクトル
varying vec3 s;  // 視線の屈折ベクトル
varying float t; // 境界面での反射率
 
void main(void)
{
  gl_FragColor = mix(textureCube(cubemap, s), textureCube(cubemap, r), t);
}

これで，こういう結果が得られます．

なんだかちょっと分かりづらいですね．環境のテクスチャが暗いせいかも知れません．そのうち環境のテクスチャを作り直して試してみたいと思います．

オレンジブック

ここまで書いてオレンジブックを見たら，まったく同じことが書いてありました orz．更に，光の分光現象を近似する手法も書いてありました．たいした手間ではなさそうなので，暇があったらこれもやってみたいと思いますが，これも環境のテクスチャを変えないとちょっと分かりづらいかも知れないなぁ．